Advertisements
Advertisements
प्रश्न
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
उत्तर

∠PST = ∠TSR ............(i)
∠PTS = ∠TSR ............(ii)(alternate angles ∵ SR || PQ)
From (i) and (ii)
∠PST = ∠PTS
Therefore,
PT = PS
But PT = QT ...(T is midpoint of PQ)
And PS = QR ...(PS and QR are opposite and equal sides of a parallelogram)
Hence,
QT = QR.
APPEARS IN
संबंधित प्रश्न
E is the mid-point of side AB and F is the mid-point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
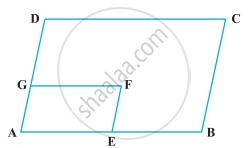
The alongside figure shows a parallelogram ABCD in which AE = EF = FC.
Prove that:
- DE is parallel to FB
- DE = FB
- DEBF is a parallelogram.
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC. 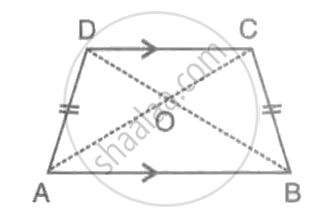
Prove that:
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.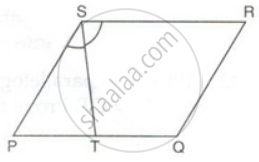
Prove that: RT bisects angle R
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.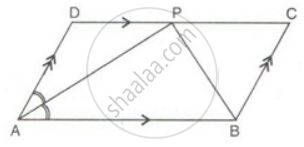
Prove that: BP bisects ∠ABC.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.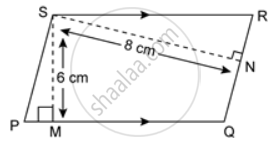
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?
In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.