Advertisements
Advertisements
Question
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
Solution

∠PST = ∠TSR ............(i)
∠PTS = ∠TSR ............(ii)(alternate angles ∵ SR || PQ)
From (i) and (ii)
∠PST = ∠PTS
Therefore,
PT = PS
But PT = QT ...(T is midpoint of PQ)
And PS = QR ...(PS and QR are opposite and equal sides of a parallelogram)
Hence,
QT = QR.
APPEARS IN
RELATED QUESTIONS
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
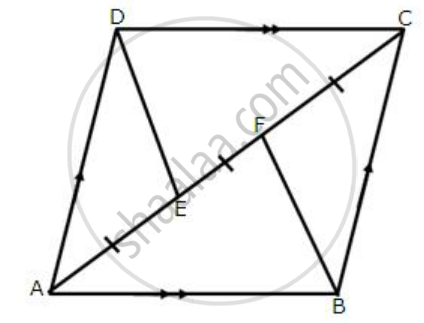
The alongside figure shows a parallelogram ABCD in which AE = EF = FC.
Prove that:
- DE is parallel to FB
- DE = FB
- DEBF is a parallelogram.
In the given figure, ABCD is a parallelogram.
Prove that: AB = 2 BC.
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC. 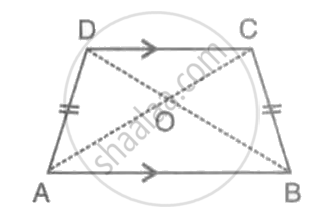
Prove that:
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD.
In parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2 AD.
Prove that:
(i) BP bisects angle B.
(ii) Angle APB = 90o.
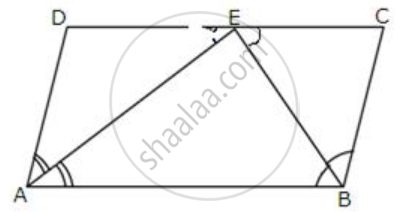
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.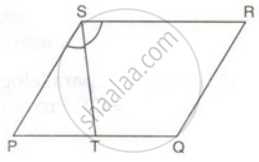
Prove that: ∠RTS = 90°
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.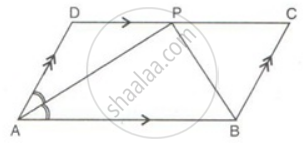
Prove that: ∠APB is a right angle.
In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.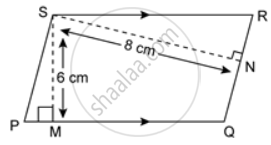
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?
Construct a parallelogram POUR in which, PO = 5.5 cm, OU = 7.2 cm and ∠O = 70°.
