Advertisements
Advertisements
Question
In parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2 AD.
Prove that:
(i) BP bisects angle B.
(ii) Angle APB = 90o.
Solution
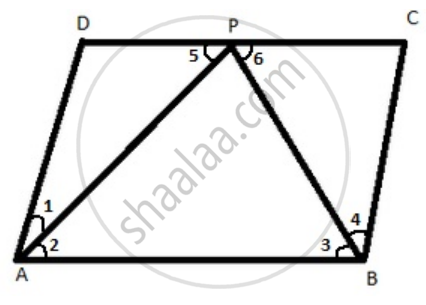
(i) Let AD = x
AB = 2AD = 2x
Also AP is the bisector ∠A
∠1 = ∠2
Now,
∠2 = ∠5 ...[ alternate angles ]
Therefore ∠1 = ∠5
Now
AP = DP = x ...[ sides opposite to equal angles are also equal ]
Therefore
AB = CD ...[ opposite sides of parallelogram are equal ]
CD = 2x
⇒ DP + PC = 2x
⇒ x + PC = 2x
⇒ PC = x
Also, BC = x
ΔBPC
⇒ ∠6 = ∠4 ...[ angles opposite to equal sides are equal ]
⇒ In ∠6 = ∠3
Therefore ∠3 =∠ 4
Hence BP bisect ∠B
(ii)
Opposite angles are supplementary
Therefore
∠1 + ∠2 + ∠3 + ∠4 = 180°
⇒ 2 ∠2 + 2 ∠3 =180° .....[ ∠1 = ∠2 , ∠3 = ∠4 ]
⇒ ∠2 + ∠3 = 90°
ΔAPB
∠2 + ∠3 ∠APB = 180°
⇒ ∠APB = 180° - 90° ...[ by angle sum property ]
⇒ ∠APB = 90°
Hence proved.
APPEARS IN
RELATED QUESTIONS
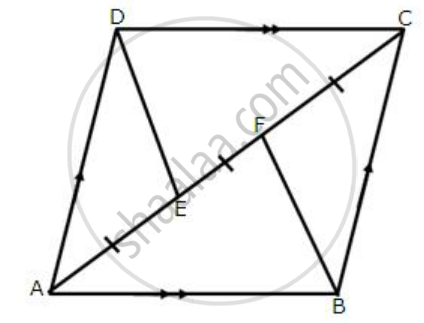
E is the mid-point of side AB and F is the mid-point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
The alongside figure shows a parallelogram ABCD in which AE = EF = FC.
Prove that:
- DE is parallel to FB
- DE = FB
- DEBF is a parallelogram.
In the alongside diagram, ABCD is a parallelogram in which AP bisects angle A and BQ bisects angle B.

Prove that:
- AQ = BP
- PQ = CD
- ABPQ is a parallelogram.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.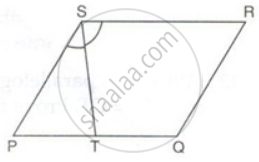
Prove that: RT bisects angle R
Find the perimeter of the parallelogram PQRS.

In the Figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to `bar("HE")` and `bar("FG")`?
In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.
Construct a parallelogram POUR in which, PO = 5.5 cm, OU = 7.2 cm and ∠O = 70°.
