Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Theorem
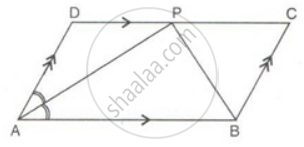
The opposite sides of a parallelogram are of equal length.
Given: ABCD is a parallelogram.
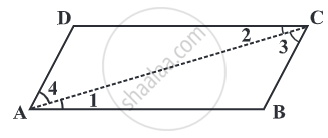
To Prove: AB = DC and BC = AD.
Construction: Draw any one diagonal, say `bar(AC)`.
Proof:
Consider a parallelogram ABCD,
In triangles ΔABC and ΔADC,
∠ 1 = ∠2, ∠ 3 = ∠ 4 .....(Pair of alternate angle)
and `bar(AC)` is common side.
Side AC = Side AC .....(common side)
∠ 1 ≅ ∠2 .....(Pair of alternate angle)
∠ 3 ≅ ∠ 4 .....(Pair of alternate angle)
by ASA congruency condition,
∆ ABC ≅ ∆ CDA
This gives AB = DC and BC = AD.
Hence Proved.
Example
Find the perimeter of the parallelogram PQRS.

In a parallelogram, the opposite sides have the same length.
Therefore, PQ = SR = 12 cm and QR = PS = 7 cm.
So,
Perimeter = PQ + QR + RS + SP
= 12 cm + 7 cm + 12 cm + 7 cm
= 38 cm.
If you would like to contribute notes or other learning material, please submit them using the button below.
Shaalaa.com | To Prove that the Opposite Sides of a Parallelogram are of Equal length
to track your progress
Series: Property: the Opposite Sides of a Parallelogram Are of Equal Length.
0%