Advertisements
Advertisements
Question
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
Solution
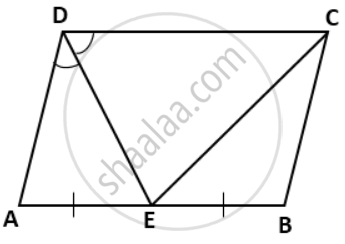
Since BC = BE
⇒ ∠BEC = ∠BCE ...(Angles opposite to equal sides are equal)
∠BEC = ∠ECD ...(Alternate angles)
⇒ ∠BCE = ∠ECD
⇒ CE is the bisector of ∠C ....(proved)
∠DCE = `(1)/(2)∠"C"` ...(Given CE bisects ∠D)
∠CDE = `(1)/(2)∠"D"` ...(Given DE bisects ∠D)
∠DCE + ∠CDE
= `(1)/(2)(∠"C" + ∠"D")`
= `(1)/(2) xx 180°` = 90°
Thus, in ΔDCE,
∠DEC = 180° - ∠DCE + ∠CDE = 180° - 90°
⇒ ∠DEC = 90°.
APPEARS IN
RELATED QUESTIONS
E is the mid-point of side AB and F is the mid-point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
The following figure shows a trapezium ABCD in which AB is parallel to DC and AD = BC. 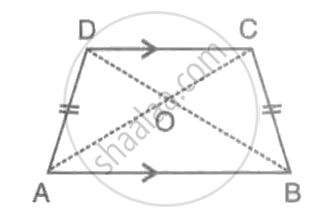
Prove that:
(i) ∠DAB = ∠CBA
(ii) ∠ADC = ∠BCD
(iii) AC = BD
(iv) OA = OB and OC = OD.
In parallelogram ABCD, the bisector of angle A meets DC at P and AB = 2 AD.
Prove that:
(i) BP bisects angle B.
(ii) Angle APB = 90o.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.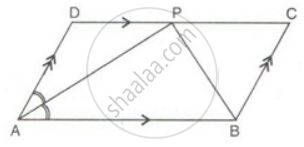
Prove that: BP bisects ∠ABC.
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.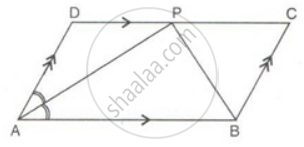
Prove that: ∠APB is a right angle.
Find the perimeter of the parallelogram PQRS.

Which of the following statement is correct?
