Advertisements
Advertisements
Question
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
Solution
Given: ABCD is a parallelogram where the diagonal BD bisects
parallelogram ABCD at angle B and D
To Prove: ABCD is a rhombus
Proof: Let us draw a parallelogram ABCD where the diagonal BD bisects the parallelogram at an angle B and D.
Construction: Let us join AC as a diagonal of the parallelogram ABCD
Since ABCD is a parallelogram in which diagonal BD bisects ∠B and ∠D
BD bisect ∠B,
∠ABD = ∠CBD = `1/2`∠ABC
BD bisect ∠D,
∠ADB = ∠CDB = `1/2`∠ABC
∴ ∠ABC = ∠ADC ...(Opposite angles of parallelogram are equal)
∴ `1/2`∠ABC = `1/2` ∠ADC
∠ABD = ∠ADB and ∠CBD = ∠CDB
∴ AD = AB and CD = BC
As ABCD is a parallelogram, opposite sides are equal
AB = CD and AD = BC
AB = BC = CD = AD
∴ ABCD is a rhombus.
APPEARS IN
RELATED QUESTIONS
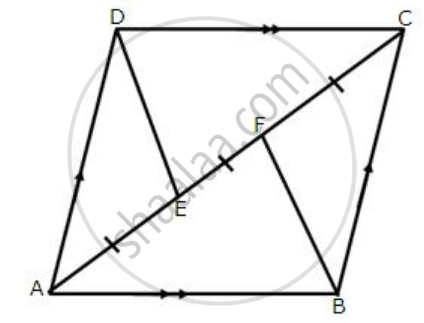
The alongside figure shows a parallelogram ABCD in which AE = EF = FC.
Prove that:
- DE is parallel to FB
- DE = FB
- DEBF is a parallelogram.
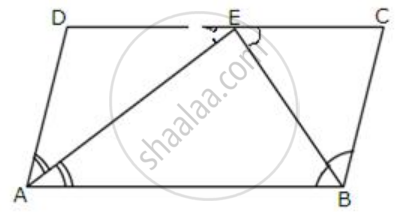
In the given figure, ABCD is a parallelogram.
Prove that: AB = 2 BC.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.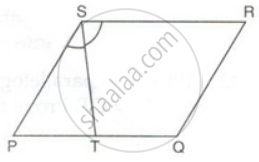
Prove that: RT bisects angle R
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.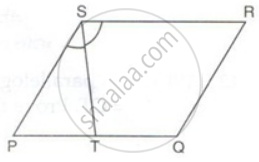
Prove that: ∠RTS = 90°
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.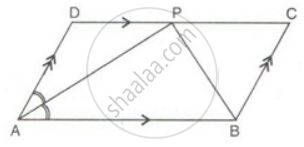
Prove that: BP bisects ∠ABC.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
Which of the following statement is correct?
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?
Construct a parallelogram POUR in which, PO = 5.5 cm, OU = 7.2 cm and ∠O = 70°.
