Advertisements
Advertisements
Question
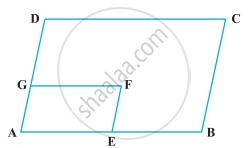
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?
Solution
BDEF is a parallelogram ...[Given]
So, BD = EF ...(i) [Opposite side of a parallelogram]
FDCE is a parallelogram ...[Given]
So, CD = EF ...(ii)
Now, from equation (i) and (ii), we get
BD = CD
APPEARS IN
RELATED QUESTIONS
In the given figure, ABCD is a parallelogram.
Prove that: AB = 2 BC.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
In the given figure, MP is the bisector of ∠P and RN is the bisector of ∠R of parallelogram PQRS. Prove that PMRN is a parallelogram.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that: BC = BE.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
In the given figure, the perimeter of parallelogram PQRS is 42 cm. Find the lengths of PQ and PS.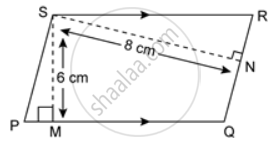
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is `9/8` of the area of the parallelogram ABCD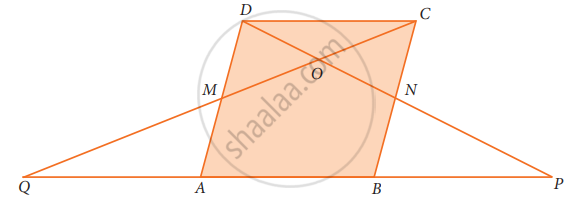
Which of the following statement is correct?
In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.