Advertisements
Advertisements
Question
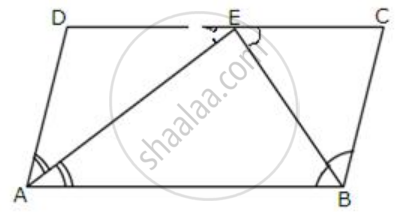
In the given figure, ABCD is a parallelogram.
Prove that: AB = 2 BC.
Solution
Given ABCD is a parallelogram
To prove: AB = 2BC

Proof: ABCD is a parallelogram
A + D + B + C = 180°
From the AEB we have
⇒ `("∠A")/(2) + ("∠B")/(2)` + E = 180°
⇒ ∠A - `("∠A")/(2)` + ∠D + ∠E1 = 180° ...[taking E1 as new angle]
⇒ ∠A + ∠D + ∠E1 = 180° + `("∠A")/(2)`
⇒ ∠E1 = `("∠A")/(2)` ...[Since ∠A + ∠D = 180°]
Again,
similarly,
∠E1 = `("∠B")/(2)`
Now
AB = DE + EC
= AD + BC
= BC + BC
= 2BC ...[since AD = BC]
Hence, proved.
APPEARS IN
RELATED QUESTIONS
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.
Prove that: QR = QT
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.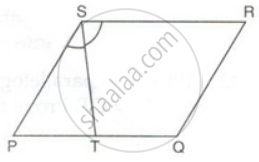
Prove that: RT bisects angle R
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.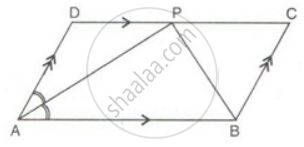
Prove that: BP bisects ∠ABC.
In the given figure, MP is the bisector of ∠P and RN is the bisector of ∠R of parallelogram PQRS. Prove that PMRN is a parallelogram.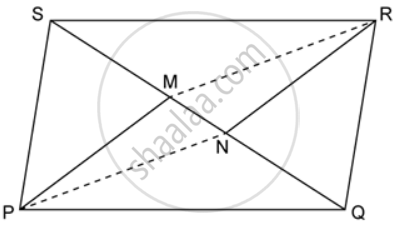
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that: BC = BE.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
Which of the following statement is correct?
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?
In the following figure, ABCD and AEFG are two parallelograms. If ∠C = 55º, determine ∠F.