Advertisements
Advertisements
Question
In parallelogram ABCD of the accompanying diagram, line DP is drawn bisecting BC at N and meeting AB (extended) at P. From vertex C, line CQ is drawn bisecting side AD at M and meeting AB (extended) at Q. Lines DP and CQ meet at O. Show that the area of triangle QPO is `9/8` of the area of the parallelogram ABCD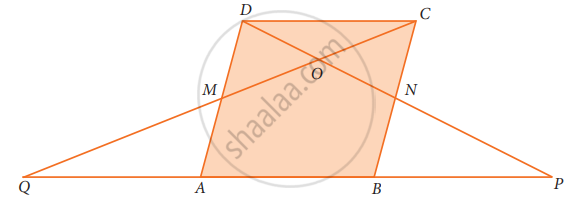
Solution
Draw OX perpendicular to QP.
In ΔADP, MN = `1/2` AP,
In ΔBCQ, MN = `1/2` QB
So, AP = BQ or AB + BP = AB + QA
∴ PB = QA
∴ QA = AB = BP or QP = QA + AB + BP = 3AB
Area of ΔOQP = `1/2 xx "QP" xx "OX"`
= `1/2 xx 3"AB" xx "OX"`
= `3/2 xx "AB" xx "OX"`
= `3/2 "AB" ("OY" + "YX")`
= `3/2 xx "AB" xx "OY" + 3/2 xx "AB" xx "YX" ...("AB" = "MN")`
= `3/2 xx "MN" xx "OY" + 3/2 xx "AB" xx "YX"`
= `3 "Area ΔOMN" + 3/2 + "Area ΔBNM"`
= `3[1/4 "area of MNCD"] + 3/2 [1/2 "area of ABCD"]`
= `3/4[1/2 "area of ABCD"] + 3/4["area of ABCD"]`
= `3/8 "area of ABCD" + 3/4 "area of ABCD"`
= area of ABCD `[3/8 + 3/4]`
= area of ABCD `((3 + 6)/8)`
= `9/8` area of ABCD.
Hence it is proved.
APPEARS IN
RELATED QUESTIONS
E is the mid-point of side AB and F is the mid-point of side DC of parallelogram ABCD. Prove that AEFD is a parallelogram.
The diagonal BD of a parallelogram ABCD bisects angles B and D. Prove that ABCD is a rhombus.
In the alongside diagram, ABCD is a parallelogram in which AP bisects angle A and BQ bisects angle B.

Prove that:
- AQ = BP
- PQ = CD
- ABPQ is a parallelogram.
Prove that the bisectors of opposite angles of a parallelogram are parallel.
Points M and N are taken on the diagonal AC of a parallelogram ABCD such that AM = CN. Prove that BMDN is a parallelogram.
PQRS is a parallelogram. T is the mid-point of PQ and ST bisects ∠PSR.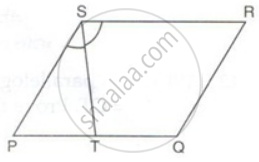
Prove that: ∠RTS = 90°
ABCD is a parallelogram. The bisector of ∠BAD meets DC at P, and AD is half of AB.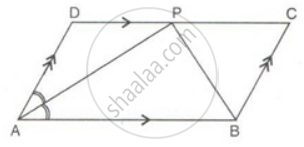
Prove that: ∠APB is a right angle.
In a parallelogram ABCD, E is the midpoint of AB and DE bisects angle D. Prove that:CE is the bisector of angle C and angle DEC is a right angle
In the Figure, ABCD is a rectangle and EFGH is a parallelogram. Using the measurements given in the figure, what is the length d of the segment that is perpendicular to `bar("HE")` and `bar("FG")`?
In the following figure, it is given that BDEF and FDCE are parallelograms. Can you say that BD = CD? Why or why not?