Advertisements
Advertisements
Question
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
Solution
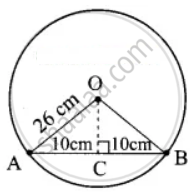
Length of the chord = 20 cm
AC = `20/2`
= 10 cm
In ΔOAC, OC2 = OA2 – AC2
= 262 – 102
= (26 + 10)(26 – 10)
= 36 × 16
OC = `sqrt(30 xx 16)`
= 6 × 4 cm
= 24 cm
Distance of the chord from the centre = 24 cm.
APPEARS IN
RELATED QUESTIONS
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Use the figure given below to fill in the blank:
R is the _______ of the circle.

State, if the following statement is true or false:
The diameters of a circle always pass through the same point in the circle.
Find the radius of the circle
Diameter = 24 cm
In figure, O is the centre of a circle, chord PQ ≅ chord RS. If ∠POR = 70° and (arc RS) = 80°, find
(i) m(arc PR)
(ii) m(arc QS)
(iii) m(arc QSR)
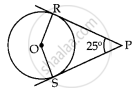
In the given figure, if ZRPS = 25°, the value of ZROS is ______
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
From the figure, identify three radii.
From the figure, identify a segment.

