Advertisements
Advertisements
प्रश्न
The diameter of the circle is 52 cm and the length of one of its chord is 20 cm. Find the distance of the chord from the centre
उत्तर
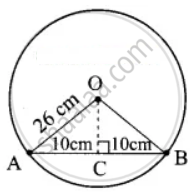
Length of the chord = 20 cm
AC = `20/2`
= 10 cm
In ΔOAC, OC2 = OA2 – AC2
= 262 – 102
= (26 + 10)(26 – 10)
= 36 × 16
OC = `sqrt(30 xx 16)`
= 6 × 4 cm
= 24 cm
Distance of the chord from the centre = 24 cm.
APPEARS IN
संबंधित प्रश्न
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC ?
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

In following fig. ABC is an equilateral triangle . A circle is drawn with centre A so that ot cuts AB and AC at M and N respectively. Prove that BN = CM.

Find the area of a circle of radius 7 cm.
AD is a diameter of a circle and AB is a chord If AD = 30 cm and AB = 24 cm then the distance of AB from the centre of the circle is
Find the radius of the circle
Diameter = 30 cm
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
Is every chord of a circle also a diameter?
