Advertisements
Advertisements
प्रश्न
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
उत्तर
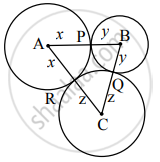
Let AP = AR = x, BP = BQ = y, CQ = CR = z .....[Radii of the same circle]
AP + BP = AB …[A – P – B]
∴ x + y = 3 …(i)
BQ + CQ = BC …[B – Q – C]
∴ y + z = 3 …(ii)
AR + CR = AC …[A – R – C]
∴ x + z = 4 …(iii)]
Adding equations (i), (ii) and (iii), we get
x + y + y + z + x + z = 3 + 3 + 4
∴ 2x + 2y + 2z = 10
∴ 2(x + y + z) = 10
∴ x + y + z = 5 …(iv)
Substituting equation (i) in equation (iv), we get 3 + z = 5
∴ z = 5 − 3
∴ z = 2 cm
Substituting equation (ii) in equation (iv), we get x + 3 = 5
∴ x = 5 − 3
∴ x = 2 cm
Substituting equation (iii) in equation (iv), we get
y + 4 = 5
∴ y = 5 − 4
∴ y = 1 cm
∴ The radii of circles with centres A, B, C are 2 cm, 1 cm and 2 cm respectively.
APPEARS IN
संबंधित प्रश्न
Write True or False. Give reasons for your answers.
If a circle is divided into three equal arcs, each is a major arc.
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
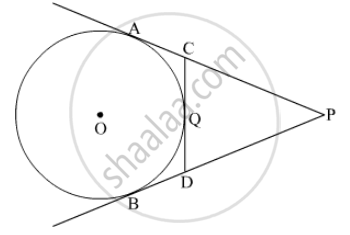
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
In the given circle with diameter AB, find the value of x.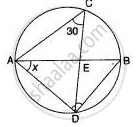
Use the figure given below to fill in the blank:
R is the _______ of the circle.

In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

In the adjoining figure, Δ ABC is circumscribing a circle. Then, the length of BC is ______
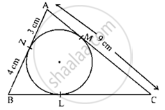
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
AB is a diameter of a circle and AC is its chord such that ∠BAC = 30°. If the tangent at C intersects AB extended at D, then BC = BD.
O is the circumcentre of the triangle ABC and D is the mid-point of the base BC. Prove that ∠BOD = ∠A.
