Advertisements
Advertisements
प्रश्न
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

उत्तर
Construction: Join OB
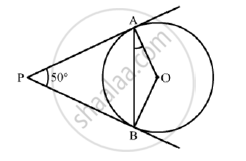
We know that the radius and tangent are perpendicular at their point of contact
∴ ∠OBP = ∠OAP = 90°
Now, In quadrilateral AOBP
∠AOB + ∠OBP + ∠APB + ∠OAP = 360° [Angle sum property of a quadrilateral]
⇒ ∠AOB + 90° + 50° + 90° = 360°
⇒ 230° + ∠BOC= 360°
⇒ ∠AOB = 130°
Now, In isosceles triangle AOB
∠AOB + ∠OAB +∠OBA =180° [Angle sum property of a triangle]
⇒ 130° + 2∠OAB = 180° [∵ ∠OAB = ∠OAB]
⇒ ∠OAB = 25°
APPEARS IN
संबंधित प्रश्न
In the given figure, the incircle of ∆ABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of ∆ABC")`
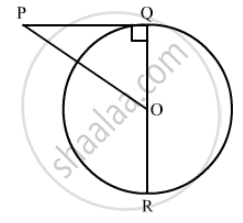
In the given figure, PO⊥QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OT are right bisector of each other.
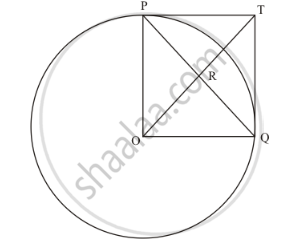
The perimeter (in cm) of a square circumscribing a circle of radius a cm, is
AB is a chord of a circle with centre O , AOC is a diameter and AT is the tangent at A as shown in Fig . 10.70. Prove that \[\angle\]BAT = \[\angle\] ACB.
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

A line segment with its end points on the circle is called a ______________
A circle of radius 3 cm can be drawn through two points A, B such that AB = 6 cm.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
