Advertisements
Advertisements
प्रश्न
AB is a chord of a circle with centre O. AOC is diameter of circle, AT is a tangent at A.
Write answers of the following questions:
- Draw the figure using the given information.
- Find the measures of ∠CAT and ∠ABC with reasons.
- Whether ∠CAT and ∠ABC are congruent? Justify your answer.
उत्तर

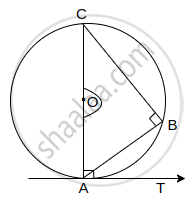
∠CAT = ∠OAT = 90° ...(By tangent theorem)
∠ABC = 90° ...(Angle in a semi-circle is right angle)- ∠CAT = ∠ABC
∠CAT ≅ ∠ABC ...[∴ The angle between a tangent of a circle and a chord drawn from the point of contact is congruent to the angle inscribed in the arc opposite to the arc intercepted by that angle.]
APPEARS IN
संबंधित प्रश्न
In Figure 1, common tangents AB and CD to the two circles with centres 01and 02 intersect at E. Prove that AB = CD.

In the given figure, PQ is a chord of length 8cm of a circle of radius 5cm. The tangents at P and Q intersect at a point T. Find the length TP

Fill in the blank
The angle between tangent at a point on a circle and the radius through the point is ........
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
true or false
Sector is the region between the chord and its corresponding arc.
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm such that the segments BC and DC into which BC is divided by the point of contact D, are of
lengths 6cm and 9cm respectively. If the area of 2 ΔABC = 54cm2 then find the lengths of sides AB and AC.

Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

In Figure 3, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB = 6 cm, BC = 9 cm and CD = 8 cm. Find the length of the side AD.
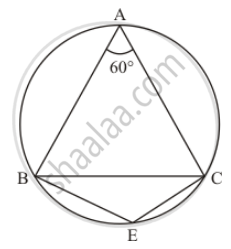
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
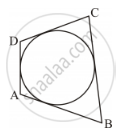
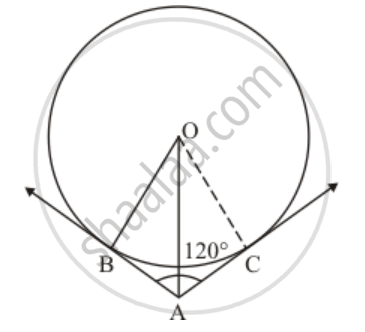
In the given figure, two tangents AB and AC are drawn to a circle with centre O such that ∠BAC = 120°. Prove that OA = 2AB.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
Draw circle with diameter: 8.4 cm
In above case, measure the length of the radius of the circle drawn.
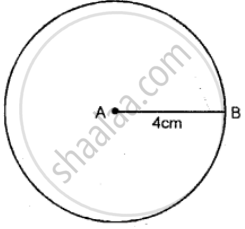
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
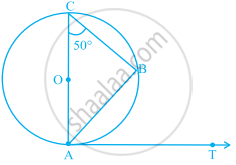
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
From the figure, identify a diameter.