Advertisements
Advertisements
प्रश्न
In figure 1, O is the centre of a circle, PQ is a chord and PT is the tangent at P.
If ∠POQ = 70°, then ∠TPQ is equal to

पर्याय
A. 55°
B. 70°
C. 45°
D. 35°
उत्तर
In ΔOPQ:
OP = OQ (Radii of same circle)
⇒ ∠OQP = ∠OPQ (Equal sides have equal angles opposite to them)
∠POQ + ∠OPQ + ∠OQP = 180° (Angle sum property of triangles)
⇒ 70° + 2∠OPQ = 180°
⇒ 2∠OPQ = 180° − 70° = 110°
⇒ ∠OPQ = 55°
It is known that the tangent is perpendicular to the radius through the point of contact.
∴ ∠OPT = 90°
⇒ ∠OPQ + ∠TPQ = 90°
⇒ 55° + ∠TPQ = 90°
⇒ ∠TPQ = 90° − 55° = 35°
The correct answer is D.
APPEARS IN
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
Fill in the blanks:
Segment of a circle is the region between an arc and __________ of the circle.
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
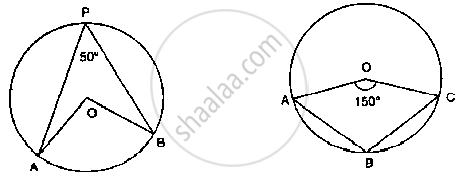
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)

Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
In the table below, write the names of the points in the interior and exterior of the circle and those on the circle.
| Diagram | Points in the interior of the circle |
Points in the exterior of the circle |
Points on the circle |
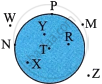 |
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
Twice the radius is ________________
