Advertisements
Advertisements
प्रश्न
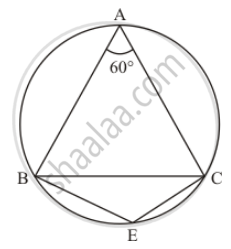
In the given figure, ΔABC is an equilateral triangle. Find m∠BEC.
उत्तर
It is given that, Δ ABC is an equilateral triangle
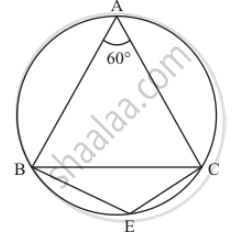
We have to find `m angle BEC`
Since Δ ABC is an equilateral triangle.
So `angle A + angle B + angle C = 180°`
And
`angle A = angleB = angleC` = 60° …… (1)
Since, quadrilateral BACE is a cyclic qualdrilateral
So , `angle A + angleE = 180°` (Sum of opposite angles of cyclic quadrilateral is 180° .)
`60° + angle E = 180°`
`angle E = 120°`
Hence
`m angle BEC = 120°`
APPEARS IN
संबंधित प्रश्न
Two circles touch each other externally at P. AB is a common tangent to the circles touching them at A and B. The value of ∠ L APB is
(A) 30°
(B) 45°
(C) 60°
(D) 90°
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
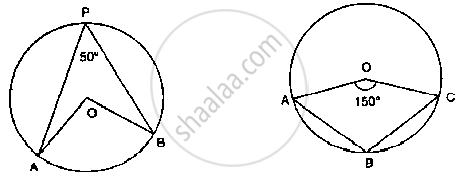
In the fig below, it is given that O is the centre of the circle and ∠AOC = 150°. Find
∠ABC.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
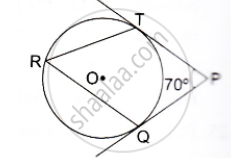
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
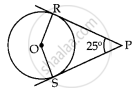
In the given figure, if ZRPS = 25°, the value of ZROS is ______
The length of tangent from an external point on a circle is always greater than the radius of the circle.
A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
