Advertisements
Advertisements
प्रश्न
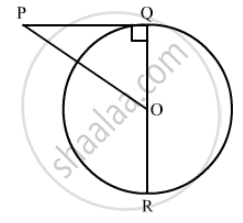
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
उत्तर
In the figure,
∠ PQD. Therefore we can use Pythagoras theorem to find the side PO.
`PO^2=PQ^2+OQ^2` …… (1)
In the problem it is given that,
`(OQ)/(PQ)=3/4`
`OQ= 3/4PQ`.....(2)
Substituting this in equation (1), we have,
`PQ^2=(9PQ^2)/16+PQ^2`
`PQ^2=(25PQ^2)/16`
`PQ^2=sqrt((25PQ^2)/16)`
`PQ=5/4PQ`........(3)
It is given that the perimeter of Δ POQis 60 cm. Therefore,
PQ + OQ + PO = 60
Substituting (2) and (3) in the above equation, we have,
`PQ+3/4PQ+5/4PQ=60`
`12/4PQ=60`
`3PQ=60`
`PQ=20`
Substituting for PQ in equation (2), we have,
`PD=5/4xx15`
`OQ=3/4xx20`
`OQ=15`
OQ is the radius of the circle and QR is the diameter. Therefore,
QR = 2OQ
QR = 30
Substituting for PQ in equation (3), we have,
`PD=5/4xx20`
`PO=25`
Thus we have found that PQ = 20 cm, QR = 30 cm and PO = 25 cm.
संबंधित प्रश्न
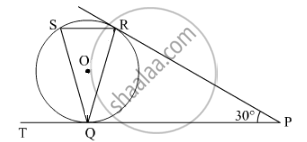
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
A circle touches the side BC of a ΔABC at a point P and touches AB and AC when produced at Q and R respectively. As shown in the figure that AQ = `1/2` (Perimeter of ΔABC).

Write True or False. Give reason for your answer.
A circle has only finite number of equal chords.
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 50° then what is the measure of ∠OAB.

If PT is a tangent to a circle with center O and PQ is a chord of the circle such that ∠QPT = 70°, then find the measure of ∠POQ.
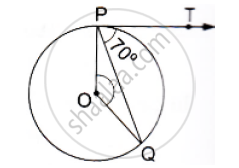
In the given figure, PQ is chord of a circle with centre O an PT is a tangent. If
∠QPT = 60°, find the ∠PRQ.

A chord of a circle of radius 14 cm subtends an angle of 120° at the centre. Find the area of the corresponding minor segment of the circle. `[User pi22/7 and sqrt3=1.73]`
On a semi-circle with AB as diameter, a point C is taken, so that m (∠CAB) = 30°. Find m(∠ACB) and m (∠ABC).
In the given figure, O is the centre of the circle and ∠DAB = 50° . Calculate the values of xand y.

If the length of a chord of a circle is 16 cm and is at a distance of 15 cm from the centre of the circle, then the radius of the circle is
In the given figure, if chords AB and CD of the circle intersect each other at right angles, then x + y =
In the given figure, BDC is a tangent to the given circle at point D such that BD = 30 cm and CD = 7 cm. The other tangents BE and CF are drawn respectively from B and C to the circle and meet when produced at A making BAC a right angle triangle. Calculate (i) AF

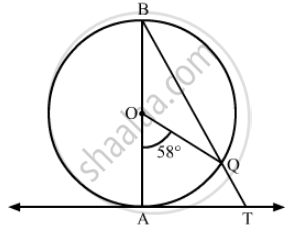
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
ABC is a triangle with AB = 10 cm, BC = 8 cm and AC = 6 cm (not drawn to scale). Three circles are drawn touching each other with the vertices as their centres. Find the radii of the three circles.

Use the figure given below to fill in the blank:
AB is a ______ of the circle.

Construct a triangle ABC with AB = 4.2 cm, BC = 6 cm and AC = 5cm. Construct the circumcircle of the triangle drawn.
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
A line segment joining any point on the circle to its center is called the _____________ of the circle
Given: A circle inscribed in a right angled ΔABC. If ∠ACB = 90° and the radius of the circle is r.
To prove: 2r = a + b – c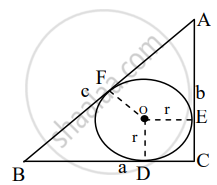
A line through the point of contact and passing through centre of the circle is known as ______
AD is a diameter of a circle and AB is a chord. If AD = 34 cm, AB = 30 cm, the distance of AB from the centre of the circle is ______.
In the given figure, O is the centre of the circle. Name all chords of the circle.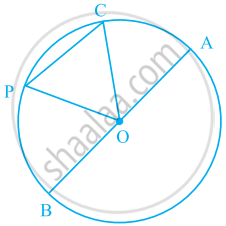
From the figure, identify a chord.

What is the area of a semi-circle of diameter ‘d’?
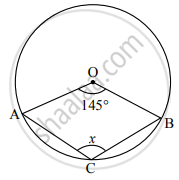
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.