Advertisements
Advertisements
Question
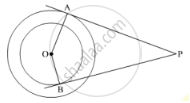
In the given figure, OQ : PQ = 3.4 and perimeter of Δ POQ = 60 cm. Determine PQ, QR and OP.
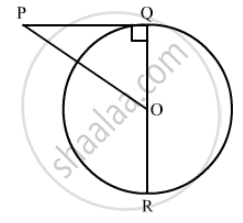
Solution
In the figure,
∠ PQD. Therefore we can use Pythagoras theorem to find the side PO.
`PO^2=PQ^2+OQ^2` …… (1)
In the problem it is given that,
`(OQ)/(PQ)=3/4`
`OQ= 3/4PQ`.....(2)
Substituting this in equation (1), we have,
`PQ^2=(9PQ^2)/16+PQ^2`
`PQ^2=(25PQ^2)/16`
`PQ^2=sqrt((25PQ^2)/16)`
`PQ=5/4PQ`........(3)
It is given that the perimeter of Δ POQis 60 cm. Therefore,
PQ + OQ + PO = 60
Substituting (2) and (3) in the above equation, we have,
`PQ+3/4PQ+5/4PQ=60`
`12/4PQ=60`
`3PQ=60`
`PQ=20`
Substituting for PQ in equation (2), we have,
`PD=5/4xx15`
`OQ=3/4xx20`
`OQ=15`
OQ is the radius of the circle and QR is the diameter. Therefore,
QR = 2OQ
QR = 30
Substituting for PQ in equation (3), we have,
`PD=5/4xx20`
`PO=25`
Thus we have found that PQ = 20 cm, QR = 30 cm and PO = 25 cm.
RELATED QUESTIONS
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Points A(–1, y) and B(5, 7) lie on a circle with centre O(2, –3y). Find the values of y. Hence find the radius of the circle.
In two concentric circles, prove that all chords of the outer circle which touch the inner circle are of equal length.
In the fig. ABC is right triangle right angled at B such that BC = 6cm and AB = 8cm. Find the radius of its in circle.
In the given figure, if arc AB = arc CD, then prove that the quadrilateral ABCD is an isosceles– trapezium (O is the centre of the circle).
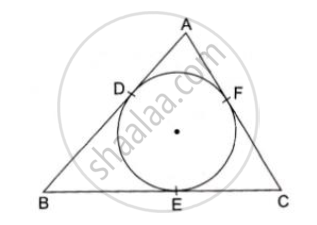
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
Tangents PA and PB are drawn from an external point P to two concentric circles with centre O and radii 8 cm and 5 cm respectively, as shown in Fig. 3. If AP = 15 cm, then find the length of BP.
In the given figure, ABCD is a cyclic quadrilateral. If ∠BCD = 100° and ∠ABD = 70°, find ∠ADB.

In the given figure, if ∠ABC = 45°, then ∠AOC =
If \[d_1 , d_2 ( d_2 > d_1 )\] be the diameters of two concentric circle s and c be the length of a chord of a circle which is tangent to the other circle , prove that\[{d_2}^2 = c^2 + {d_1}^2\].
From an external point P , tangents PA = PB are drawn to a circle with centre O . If \[\angle PAB = {50}^o\] , then find \[\angle AOB\]
Two concentric circles are of diameters 30 cm and 18 cm. Find the length of the chord of the larger circle which touches the smaller circle.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
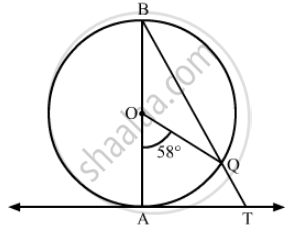
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
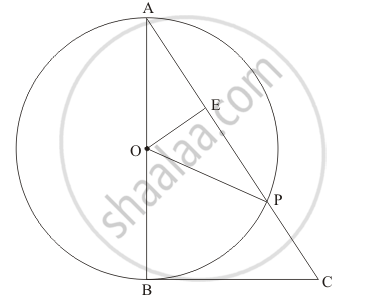
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
In the given figure, seg MN is a chord of a circle with centre O. MN = 25, L is a point on chord MN such that ML = 9 and d(O,L) = 5. Find the radius of the circle.
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Use the figure given below to fill in the blank:
R is the _______ of the circle.

Use the figure given below to fill in the blank:
Diameter of a circle is ______.

The diameter of a circle is 12.6 cm. State, the length of its radius.
In the figure, a circle touches all the sides of quadrilateral ABCD from the inside. The center of the circle is O. If AD⊥ DC and BC = 38, QB = 27, DC = 25, then find the radius of the circle.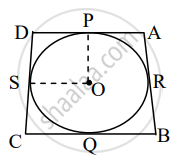
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

If a chord AB subtends an angle of 60° at the centre of a circle, then angle between the tangents at A and B is also 60°.
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
A circle of radius 3 cm with centre O and a point L outside the circle is drawn, such that OL = 7 cm. From the point L, construct a pair of tangents to the circle. Justify LM and LN are the two tangents.
