Advertisements
Advertisements
Question
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
Solution
Let ABCD be the quadrilateral circumscribing the circle.
Let E, F, G and H be the points of contact of the quadrilateral to the circle.

To Prove: AB + DC = AD + BC
Proof:
AB = AE + EB
AD = AH + HD
DC = DG + GC
BC = BF + FC
We have:
AE = AH (Tangents drawn from an external point to the circle are equal.)
Similarly, we have:
BE = BF
DH = DG
CG = CF
Now, we have:
AB + DC = AE + EB + DG + GC
= AH + BF + DH + CF
= (AH + DH) + (BF + CF)
= AD + BC
⇒ AB + DC = AD + BC
Thus, if a quadrilateral is drawn to circumscribe a circle, the sums of opposite sides are equal.
Hence, proved.
APPEARS IN
RELATED QUESTIONS
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
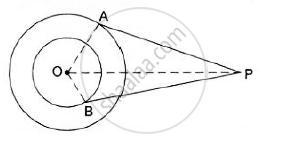
In the given figure, O is the centre of the two concentric circles of radii 4 cm and 6cm respectively. AP and PB are tangents to the outer and inner circle respectively. If PA = 10cm, find the length of PB up to one place of the decimal.
The greatest chord of a circle is called its
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
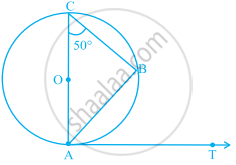
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB = 50°. If AT is the tangent to the circle at point A, then ∠BAT is equal to ______.
If radius of a circle is 5 cm, then find the length of longest chord of a circle.
What is the area of a semi-circle of diameter ‘d’?
Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2π × radius of a circle.
