Advertisements
Advertisements
प्रश्न
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
उत्तर
Let ABCD be the quadrilateral circumscribing the circle.
Let E, F, G and H be the points of contact of the quadrilateral to the circle.

To Prove: AB + DC = AD + BC
Proof:
AB = AE + EB
AD = AH + HD
DC = DG + GC
BC = BF + FC
We have:
AE = AH (Tangents drawn from an external point to the circle are equal.)
Similarly, we have:
BE = BF
DH = DG
CG = CF
Now, we have:
AB + DC = AE + EB + DG + GC
= AH + BF + DH + CF
= (AH + DH) + (BF + CF)
= AD + BC
⇒ AB + DC = AD + BC
Thus, if a quadrilateral is drawn to circumscribe a circle, the sums of opposite sides are equal.
Hence, proved.
APPEARS IN
संबंधित प्रश्न
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
In following figure, three circles each of radius 3.5 cm are drawn in such a way that each of them touches the other two. Find the area enclosed between these three circles (shaded region). `["Use" pi=22/7]`

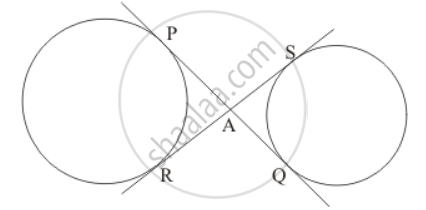
In the given figure, common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
If the radius of a circle is 5 cm, what will its diameter be?
Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord
A part of circumference of a circle is called as _______
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

The length of the tangent from point A to a circle, of radius 3 cm, is 4 cm. The distance of A from the centre of the circle is ______
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
