Advertisements
Advertisements
प्रश्न
A quadrilateral is drawn to circumscribe a circle. Prove that the sums of opposite sides are equal ?
उत्तर
Let ABCD be the quadrilateral circumscribing the circle.
Let E, F, G and H be the points of contact of the quadrilateral to the circle.

To Prove: AB + DC = AD + BC
Proof:
AB = AE + EB
AD = AH + HD
DC = DG + GC
BC = BF + FC
We have:
AE = AH (Tangents drawn from an external point to the circle are equal.)
Similarly, we have:
BE = BF
DH = DG
CG = CF
Now, we have:
AB + DC = AE + EB + DG + GC
= AH + BF + DH + CF
= (AH + DH) + (BF + CF)
= AD + BC
⇒ AB + DC = AD + BC
Thus, if a quadrilateral is drawn to circumscribe a circle, the sums of opposite sides are equal.
Hence, proved.
APPEARS IN
संबंधित प्रश्न
Two circles touch externally at a point P. from a point T on the tangent at P, tangents TQ and TR are drawn to the circles with points of contact Q and E respectively. Prove that TQ = TR.
Fill in the blank:
An arc is a ................ when its ends are the ends of a diameter.
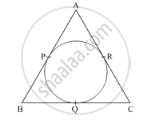
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
If the area of a circle is equal to sum of the areas of two circles of diameters 10 cm and 24 cm, then the diameter of the larger circle (in cm) is:
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.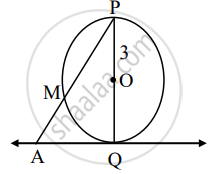
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

In the given figure, point P is 26 cm away from the centre O of a circle and the length PT of the tangent drawn from P to the circle is 24 cm. Then the radius of the circle is ______
In the following figure, if ∠ABC = 20º, then ∠AOC is equal to ______.