Advertisements
Advertisements
प्रश्न
Find the length of the chord of a circle in the following when:
Radius is 6.5 cm and the distance from the centre is 2.5 cm
उत्तर
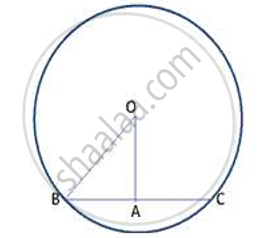
BA = AC ----(1) (Perpendicular from centre to a chord bisects the chord)
In right Δ OAB,
By Pythagoras theorem, OB2 = OA2 + AB2
AB2 = 6.52 + 2.52
= 42.25 - 6.25 = 36
AB = 6cm
∴ Length of chord BC = 2 AB (from (1))
= 2 (6) = 12 cm
APPEARS IN
संबंधित प्रश्न
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
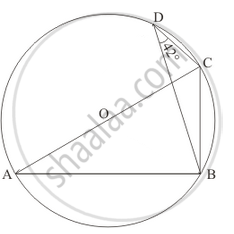
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
If all the sides of a parallelogram touch a circle, show that the parallelogram is a rhombus.
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

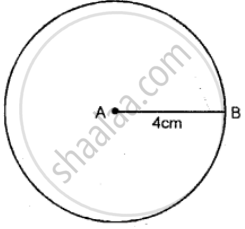
Mark two points A and B ,4cm a part, Draw a circle passing through B and with A as a center
A line through the point of contact and passing through centre of the circle is known as ______
In the given figure, AB is the diameter of the circle. Find the value of ∠ACD.