Advertisements
Advertisements
प्रश्न
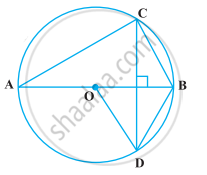
In the given figure, O is the centre of the circle and ∠BDC = 42°. The measure of ∠ACB is
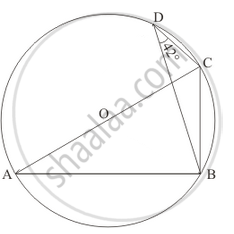
विकल्प
42°
48°
58°
52°
उत्तर
48°
Construction: Join A and D.
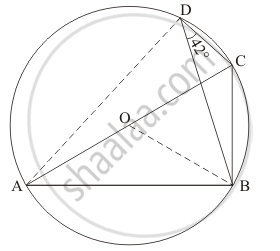
Since AC is the diameter. So ∠ADC will be 90°.
Therefore,
`angleADB = 90 - angleBDC`
= 90 - 42
`angle ADB = 48°`
∠ACB = ∠ADB = 48° (Angle in the same segment are equal.)
APPEARS IN
संबंधित प्रश्न
If from any point on the common chord of two intersecting circles, tangents be drawn to circles, prove that they are equal.
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
In two concentric circles, a chord of length 8 cm of the large circle touches the smaller circle. If the radius of the larger circle is 5 cm, then find the radius of the smaller circle.
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Find the length of the chord AC where AB and CD are the two diameters perpendicular to each other of a circle with radius `4sqrt(2)` cm and also find ∠OAC and ∠OCA
In a circle, AB and CD are two parallel chords with centre O and radius 10 cm such that AB = 16 cm and CD = 12 cm determine the distance between the two chords?
The length of tangent from an external point on a circle is always greater than the radius of the circle.
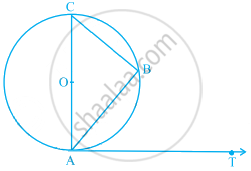
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.
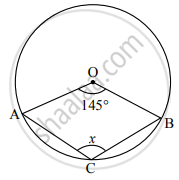
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.