Advertisements
Advertisements
प्रश्न
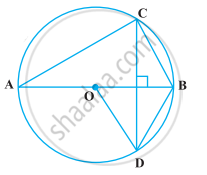
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.
उत्तर
Given, in the figure BD = OD, CD ⊥ AB.
In ΔOBD, BD = OD ...[Given]
OD = OB ...[Both are the radius of circle]
∴ OB = OD = BD
Thus, ΔODB is an equilateral triangle.
∴ ∠BOD = ∠OBD = ∠ODB = 60°
In ΔMBC and ΔMBD,
MB = MB ...[Common side]
∠CMB = ∠BMD = 90°
And CM = MD ...[In a circle, any perpendicular drawn on a chord also bisects the chord]
∴ ΔMBC ≅ ΔMBD ...[By SAS congruence rule]
∴ ∠MBC = ∠MBD ...[By CPCT]
⇒ ∠MBC = ∠OBD = 60° ...[∵ ∠OBD = 60°]
Since, AB is a diameter of the circle.
∴ ∠ACB = 90°
In ΔACB, ∠CAB + ∠CBA + ∠ACB = 180° ...[By angle sum property of a triangle]
⇒ ∠CAB + 60° + 90° = 180°
⇒ ∠CAB = 180° – (60° + 90°) = 30°
APPEARS IN
संबंधित प्रश्न
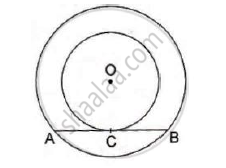
In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the lengths of TP and TQ.

A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.
Choose correct alternative answer and fill in the blank.
Radius of a circle is 10 cm and distance of a chord from the centre is 6 cm. Hence the length of the chord is .........
The point of concurrence of all angle bisectors of a triangle is called the ______.
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
C(O, r1) and C(O, r2) are two concentric circles with r1 > r2 AB is a chord of C(O, r1) touching C(O, r2) at C then ______
The tangent at a point C of a circle and a diameter AB when extended intersect at P. If ∠PCA = 110°, find ∠CBA see figure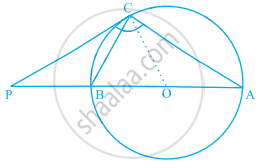
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
