Advertisements
Advertisements
Question
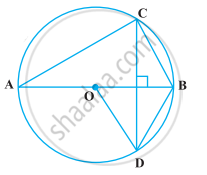
In the following figure, O is the centre of the circle, BD = OD and CD ⊥ AB. Find ∠CAB.
Solution
Given, in the figure BD = OD, CD ⊥ AB.
In ΔOBD, BD = OD ...[Given]
OD = OB ...[Both are the radius of circle]
∴ OB = OD = BD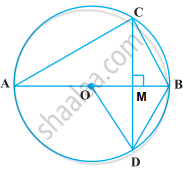
Thus, ΔODB is an equilateral triangle.
∴ ∠BOD = ∠OBD = ∠ODB = 60°
In ΔMBC and ΔMBD,
MB = MB ...[Common side]
∠CMB = ∠BMD = 90°
And CM = MD ...[In a circle, any perpendicular drawn on a chord also bisects the chord]
∴ ΔMBC ≅ ΔMBD ...[By SAS congruence rule]
∴ ∠MBC = ∠MBD ...[By CPCT]
⇒ ∠MBC = ∠OBD = 60° ...[∵ ∠OBD = 60°]
Since, AB is a diameter of the circle.
∴ ∠ACB = 90°
In ΔACB, ∠CAB + ∠CBA + ∠ACB = 180° ...[By angle sum property of a triangle]
⇒ ∠CAB + 60° + 90° = 180°
⇒ ∠CAB = 180° – (60° + 90°) = 30°
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
The centre of a circle lies in ____________ of the circle.
Fill in the blanks:
The longest chord of a circle is a __________ of the circle.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
Fill in the blank
Circles having the same centre and different radii are called ...........................circles.
Prove that two different circles cannot intersect each other at more than two points.
A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
Find the diameter of the circle
Radius = 10 cm
If a number of circles pass through the endpoints P and Q of a line segment PQ, then their centres lie on the perpendicular bisector of PQ.
