Advertisements
Advertisements
Question
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.

Solution
It is given that, ABCD is cyclic quadrilateral in which AD || BC
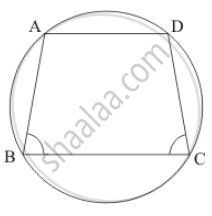
We have to prove `angleB = angle C`
Since, ABCD is a cyclic quadrilateral
So,
`angle B + angle D = 180°` and `angle A + angle C = 180°` ..… (1)
`⇒ angleB + angle A ` = 180° and `angle C + angle D = 180°` (Sum of pair of consecutive interior angles is 180°) …… (2)
From equation (1) and (2) we have
`angleB + angleD + angleB + angle A ` = 360° …… (3)
`angleA + angleC + angleC + angle D ` = 360° …… (4)
`2angleB + angleD + angleA = 2 angleC + angleA + angleD`
`2angleB = 2angleC`
`angleB = angleC`
Hence Proved
APPEARS IN
RELATED QUESTIONS
In fig common tangents PQ and RS to two circles intersect at A. Prove that PQ = RS.
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
A triangle PQR is drawn to circumscribe a circle of radius 8 cm such that the segments QT and TR, into which QR is divided by the point of contact T, are of lengths 14 cm and 16 cm respectively. If area of ∆PQR is 336 cm2, find the sides PQ and PR.
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
State, if the following statement is true or false:
The longest chord of a circle is its diameter.
The chord of length 30 cm is drawn at the distance of 8 cm from the centre of the circle. Find the radius of the circle
The radius of a circle of diameter 24 cm is _______
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
