Advertisements
Advertisements
Question
AB and CD are common tangents to two circles of equal radii. Prove that AB = CD.
Solution
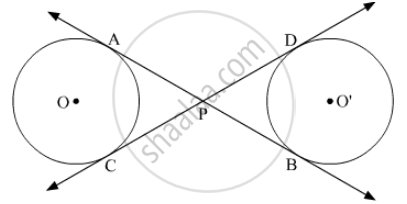
Given: Two circles with centre’s O and O'. AB and CD are common tangents to the circles which intersect in P.
To Prove: AB = CD
Proof:
AP = PC (length of tangents drawn from an external point to the circle are equal) ..… (1)
PB = PD (length of tangents drawn from an external point to the circle are equal) ..… (2)
Adding (1) and (2), we get
AP + PB = PC + PD
⇒ AB = CD
Hence Proved
APPEARS IN
RELATED QUESTIONS
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

A point P is 25 cm away from the center of a circle and the length of tangent drawn from P to the circle is 24 cm. Find the radius of the circle.
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
Radius of a circle with centre O is 4 cm. If l(OP) = 4.2 cm, say where point P will lie.
If O is the centre of the circle, find the value of x in each of the following figures

State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
Draw circle with the radii given below.
2 cm
From a point P which is at a distance of 13 cm from the centre O of a circle of radius 5 cm, the pair of tangents PQ and PR to the circle are drawn. Then the area of the quadrilateral PQOR is ______
The circumcentre of the triangle ABC is O. Prove that ∠OBC + ∠BAC = 90º.
