Advertisements
Advertisements
Question
In the below fig. O is the centre of the circle. If ∠APB = 50°, find ∠AOB and ∠OAB.

Solution
ΔAPB = 50°
By degree measure theorem
∠AOB=2 ∠APB
⇒∠APB= 2 × 50° = 100°
Since OA =OB
[ Radius of circle ]
Then ∠OAB=∠OBA
[ Angle's opposite to equal sides ]
Let ∠OAB = x
In Δ OAB by angle sum property
`∠OAB+∠OBA+∠AOB=180°`
`⇒x+x+100=180°`
`⇒2x+100=180°`
`⇒2x=80°`
`⇒x=40°`
`∠OAB =∠OBA= 40°`
APPEARS IN
RELATED QUESTIONS
Prove that the line segment joining the points of contact of two parallel tangents of a circle, passes through its centre.
Write True or False. Give reason for your answer.
A circle is a plane figure.
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
true or false
Sector is the region between the chord and its corresponding arc.
In the given figure, O is the centre of the circle. Find ∠CBD.

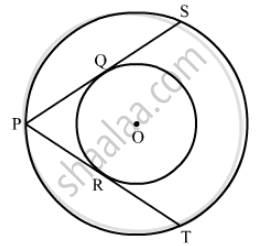
In Fig. 8.78, there are two concentric circles with centre O. PRT and PQS are tangents to the inner circle from a point P lying on the outer circle. If PR = 5 cm, find the length of PS.
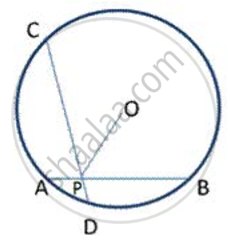
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
Use the figure given below to fill in the blank:
R is the _______ of the circle.

In the adjoining figure, seg DE is the chord of the circle with center C. seg CF⊥ seg DE and DE = 16 cm, then find the length of DF?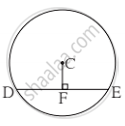
If d1, d2 (d2 > d1) be the diameters of two concentric circles and c be the length of a chord of a circle which is tangent to the other circle, then ______
