Advertisements
Advertisements
Question
A circular park of radius 40 m is situated in a colony. Three boys Ankur, Amit and Anand are sitting at equal distance on its boundary each having a toy telephone in his hands to talk
to each other.
Solution
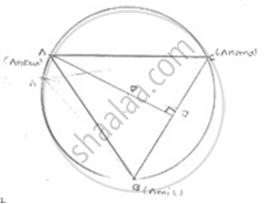
Given hat AB = BC = CA
So, ABC is an equilateral triangle
OA (radius) = 40m.
Medians of equilaterals triangles pass through the circum center (0) of the equilaterals
triangles ABC
We also know that median intersect each other at the 2 :1As AD is the median of equilaterals triangle ABC, we can write:
`(OA)/(OD)-2/7`
`⇒(40m)/(OD)-2/7`
`∴AD=OA+OD=(40+20)m`
`=60m`
In ΔADC
By using Pythagoras theorem
`AC^2=AD^2+DC^2`
`AC^2=AD^2+DC^2`
`AC^2=(60)^2+((AC)/2)^2`
`AC^2=3600+(AC^2)/4`
`⇒3/2AC^2=3600`\
`⇒AC^2=4800`
`⇒AC^2=40sqrt3m`
So, length of string of each phone will be `40sqrt3m`
APPEARS IN
RELATED QUESTIONS
Draw different pairs of circles. How many points does each pair have in common? What is the maximum number of common points?
Fill in the blank:
All points lying inside/outside a circle are called .................. points/ .....................points.
true or false
Line segment joining the centre to any point on the circle is a radius of the circle,
Give a method to find the centre of a given circle.
Prove that any three points on a circle cannot be collinear.
Choose the correct alternative:
If the points, A, B, C are non-collinear points, then how many circles can be drawn which passes through points A, B, and C?
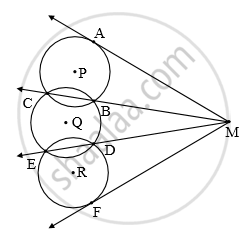
In the above figure, the circles with P, Q, and R intersect at points B, C, D, and E as shown. Lines CB and ED intersect in point M. Lines are drawn from point M to touch the circles at points A and F. Prove that MA = MF.
Four alternative answers for the following question is given. Choose the correct alternative.
How many circles can drawn passing through three non-collinear points?
How many circles can be drawn passing through a point?
Find the value of y, if the points A(3, 4), B(6, y) and C(7, 8) are collinear.
