Topics
Similarity
- Similarity of Triangles
- Properties of Ratios of Areas of Two Triangles
- Basic Proportionality Theorem (Thales Theorem)
- Converse of Basic Proportionality Theorem
- Property of an Angle Bisector of a Triangle
- Property of Three Parallel Lines and Their Transversals
- Similar Triangles
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
Pythagoras Theorem
- Pythagoras Theorem
- Pythagorean Triplet
- Property of 30°- 60°- 90° Triangle Theorem
- Property of 45°- 45°- 90° Triangle Theorem
- Similarity in Right Angled Triangles
- Theorem of Geometric Mean
- Right-angled Triangles and Pythagoras Property
- Converse of Pythagoras Theorem
- Application of Pythagoras Theorem in Acute Angle and Obtuse Angle
- Apollonius Theorem
Circle
- Concept of Circle
- Circles Passing Through One, Two, Three Points
- Secant and Tangent
- Tangent to a Circle
- Converse of Tangent Theorem
- Tangent Segment Theorem
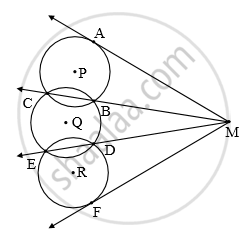
- Touching Circles
- Theorem of Touching Circles
- Tangent Properties - If Two Circles Touch, the Point of Contact Lies on the Straight Line Joining Their Centers
- Introduction to an Arc
- Congruence of Arcs
- Property of Sum of Measures of Arcs
- Inscribed Angle
- Intercepted Arc
- Inscribed Angle Theorem
- Corollaries of Inscribed Angle Theorem
- Cyclic Quadrilateral
- Theorem: Opposite angles of a cyclic quadrilateral are supplementary.
- Corollary of Cyclic Quadrilateral Theorem
- Converse: If a Pair of Opposite Angles of a Quadrilateral is Supplementary, Then the Quadrilateral is Cyclic.
- Converse of Cyclic Quadrilateral Theorem
- Theorem of Angle Between Tangent and Secant
- Converse of Theorem of the Angle Between Tangent and Secant
- Theorem of Internal Division of Chords
- Theorem of External Division of Chords
- Tangent Secant Segments Theorem
- Tangent - Secant Theorem
- Angle Subtended by the Arc to the Point on the Circle
- Angle Subtended by the Arc to the Centre
- Number of Tangents from a Point on a Circle
Geometric Constructions
- Basic Geometric Constructions
- Division of a Line Segment
- Construction of Similar Triangle
- Construction of a Tangent to the Circle at a Point on the Circle
- To Construct Tangents to a Circle from a Point Outside the Circle.
Co-ordinate Geometry
- Coordinate Geometry
- Distance Formula
- Intercepts Made by a Line
- Division of a Line Segment
- Section Formula
- The Mid-point of a Line Segment (Mid-point Formula)
- Centroid Formula
- Slope of a Line
- General Equation of a Line
- Standard Forms of Equation of a Line
Trigonometry
Mensuration
- Conversion of Solid from One Shape to Another
- Euler's Formula
- Concept of Surface Area, Volume, and Capacity
- Surface Area and Volume of Three Dimensional Figures
- Surface Area and Volume of Different Combination of Solid Figures
- Frustum of a Cone
- Sector of a Circle
- Area of a Sector of a Circle
- Length of an Arc
- Segment of a Circle
- Area of a Segment
- Circumference of a Circle
- Areas of Sector and Segment of a Circle
- Infinite circles pass through one point.
- Infinite circles pass through two distinct points.
- There is a unique circle passing through three non-collinear points.
- No circle can pass through 3 collinear points.
Notes
We know that through one point say 'P' we can draw many circles.

Through two point say 'P' and 'Q' again we can draw many circles.
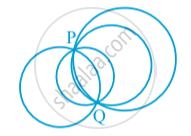
Now take three points 'A' , 'B' and 'C'.
After drawing perpendicular bisector AB on 'PQ' and RS on 'BC', we find that OA = OB = OC.
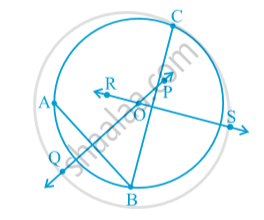
Where O is the point where both the perpendicular bisector meet.
Now a circle can be drawn by taking O as a centre and OA as a radius. This demonstration proves the theorem that There is one and only one circle passing through three given non-collinear points.
This circle is called the circumcircle of the ∆ ABC. Its centre and radius are called respectively the circumcentre and the circumradius of the triangle.
Theorem
Theorem : There is one and only one circle passing through three given non-collinear points.
Proof : 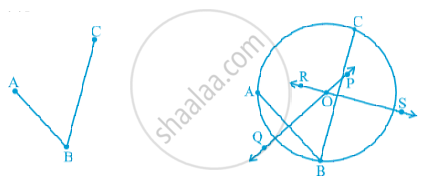
Given : We have three non -collinear points A , B and C (As shown e fig.)
To prove : We need to prove that there is ONE and ONLY one circle that passes through all the three points A , B and C.
We join AB and BC . Then we draw a perpendicular bisector of AB say line QP . Also draw a perpendicular bisector of BC say line RS .
Since AB and BC are not parallel , their perpendicular bisector i.e. line QP and line RS will not be parallel. Say line QP and line RS intersect at point O.
Now we know that if we take any point on the perpendicular bisector of AB , that point will be equidistant from both A and B . So, O is on line QP.
Therefore , OA = OB .....(1)
Similarly , if we take any point on the perpendicular bisector of BC , that point will be equidistance from both B and C. So, o is on line RS.
Therefore, OB = OC ....(2)
From (1) and (2) , we get
OA =OB =OC
We see that O is such a point that is equidistant from all three points A,B and C. So, we can draw a circle with centre O and radius OA that will passed through B and C (since OA =OB = OC).
Since O is a unique point i.e. the point of intersection of perpendicular bisectors of AB and BC and we saw that OA=OB = OC , we can say that there is ONE and OnLY one circle that passes through all three non - collinear points.
Hence proved.