Topics
Similarity
- Similarity of Triangles
- Properties of Ratios of Areas of Two Triangles
- Basic Proportionality Theorem (Thales Theorem)
- Converse of Basic Proportionality Theorem
- Property of an Angle Bisector of a Triangle
- Property of Three Parallel Lines and Their Transversals
- Similar Triangles
- Criteria for Similarity of Triangles
- Areas of Similar Triangles
Pythagoras Theorem
- Pythagoras Theorem
- Pythagorean Triplet
- Property of 30°- 60°- 90° Triangle Theorem
- Property of 45°- 45°- 90° Triangle Theorem
- Similarity in Right Angled Triangles
- Theorem of Geometric Mean
- Right-angled Triangles and Pythagoras Property
- Converse of Pythagoras Theorem
- Application of Pythagoras Theorem in Acute Angle and Obtuse Angle
- Apollonius Theorem
Circle
- Concept of Circle
- Circles Passing Through One, Two, Three Points
- Secant and Tangent
- Tangent to a Circle
- Converse of Tangent Theorem
- Tangent Segment Theorem
- Touching Circles
- Theorem of Touching Circles
- Tangent Properties - If Two Circles Touch, the Point of Contact Lies on the Straight Line Joining Their Centers
- Introduction to an Arc
- Congruence of Arcs
- Property of Sum of Measures of Arcs
- Inscribed Angle
- Intercepted Arc
- Inscribed Angle Theorem
- Corollaries of Inscribed Angle Theorem
- Cyclic Quadrilateral
- Theorem: Opposite angles of a cyclic quadrilateral are supplementary.
- Corollary of Cyclic Quadrilateral Theorem
- Converse: If a Pair of Opposite Angles of a Quadrilateral is Supplementary, Then the Quadrilateral is Cyclic.
- Converse of Cyclic Quadrilateral Theorem
- Theorem of Angle Between Tangent and Secant
- Converse of Theorem of the Angle Between Tangent and Secant
- Theorem of Internal Division of Chords
- Theorem of External Division of Chords
- Tangent Secant Segments Theorem
- Tangent - Secant Theorem
- Angle Subtended by the Arc to the Point on the Circle
- Angle Subtended by the Arc to the Centre
- Number of Tangents from a Point on a Circle
Geometric Constructions
- Basic Geometric Constructions
- Division of a Line Segment
- Construction of Similar Triangle
- Construction of a Tangent to the Circle at a Point on the Circle
- To Construct Tangents to a Circle from a Point Outside the Circle.
Co-ordinate Geometry
- Coordinate Geometry
- Distance Formula
- Intercepts Made by a Line
- Division of a Line Segment
- Section Formula
- The Mid-point of a Line Segment (Mid-point Formula)
- Centroid Formula
- Slope of a Line
- General Equation of a Line
- Standard Forms of Equation of a Line
Trigonometry
Mensuration
- Conversion of Solid from One Shape to Another
- Euler's Formula
- Concept of Surface Area, Volume, and Capacity
- Surface Area and Volume of Three Dimensional Figures
- Surface Area and Volume of Different Combination of Solid Figures
- Frustum of a Cone
- Sector of a Circle
- Area of a Sector of a Circle
- Length of an Arc
- Segment of a Circle
- Area of a Segment
- Circumference of a Circle
- Areas of Sector and Segment of a Circle
- Ratio of areas of two triangles is equal to the ratio of the products of their bases and corresponding heights.
- Areas of triangles with equal heights are proportional to their corresponding bases.
- Areas of triangles with equal bases are proportional to their corresponding heights.
Notes
We have studied Ratio and Proportion. The statement, "the numbers a and b are in the ratio m/n " is also written as, "the numbers a and b are in proportion m:n". For this concept we consider positive real numbers. We know that the lengths of line segments and area of any figure are positive real numbers. We know the formula of area of a triangle.
Area of a triangle =1/2 Base × Height
Let’s find the ratio of areas of any two triangles.
Ex. In D ABC, AD is the height and BC is the base. In D PQR, PS is the height and QR is the base.
`A(triangle ABC)/A(trianglePQR)=(1/2xxBCxxAD)/(1/2xxQRxxPS)`
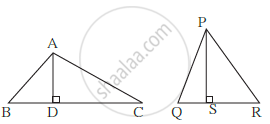
`A(triangle ABC)/A(triangle PQR)=(BCxxAD)/(QRxxPS)`
Hence the ratio of the areas of two triangles is equal to the ratio of the products of their bases and corrosponding heights. Base of a triangle is b1 and height is h1. Base of another triangle is b2 and height is h2 .
Then the ratio of their areas =`(b_1xxh_1)/(b_2xxh_2)`
Suppose some conditions are imposed on these two triangles,
Condition 1: If the heights of both triangles are equal then :
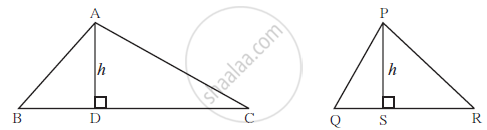
`A(triangle ABC)/A(triangle PQR)=(BCxxh)/(QRxxh)="BC"/QR"`
`A(triangle ABC)/A(triangle PQR)=b_1/b_2`
Property: The ratio of the areas of two triangles with equal heights is equal to the ratio of their corresponding bases.
Condition 2: If the bases of both triangles are equal then -
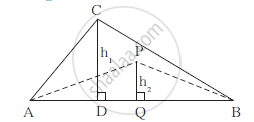
`A(triangle ABC)/A(triangle APB)=(ABxxh_1)/(ABxxh_2)`
`A(triangle ABC)/A(triangle APB)=h_1/h_2`
Property: The ratio of the areas of two triangles with equal bases is equal to the ratio of their corresponding heights.