Advertisements
Advertisements
Question
In the fig. a circle is inscribed in a quadrilateral ABCD in which ∠B = 90° if AD = 23cm,
AB = 29cm and DS = 5cm, find the radius of the circle.
Solution
Given AD = 23 cm
AB = 29 cm
∠B = 90°
DS = 5cm
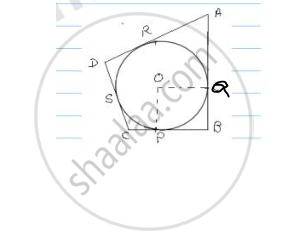
From fig in quadrilateral POQB
∠OPB = ∠OQB = 90° = ∠B = ∠POQ
and PO = OQ. ∴ POQB is a square PB = BQ = r
We know that
Tangents drawn from external point to circle are equal in length.
We know that
Tangents drawn from external point to circle are equal in length.
From A, AR = AQ …. (i)
From B, PB = QB …. (ii)
From C, PC = CS …. (iii)
From D, DR = DS …. (iv)
(i) + (ii) + (iv) ⇒ AR + DB + DR = AQ + QB + DS
⇒ (AR + DR) + r = (AQ + QB) + DS
AD + r = AB + DS
⇒ 23 + r = 29 + 5
⇒ r = 34 – 23 = 11 cm
∴ radius = 11 cm
APPEARS IN
RELATED QUESTIONS
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
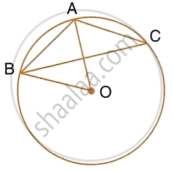
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
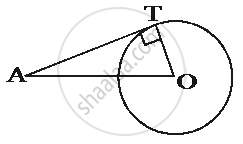
A is a point at a distance 13 cm from the centre O of a circle of radius 5 cm. AP and AQ are the tangents to the circle at P and Q. If a tangent BC is drawn at a point R lying on the minor arc PQ to intersect AP at B and AQ at C, find the perimeter of the ∆ABC.

In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Draw two circles of different radii. How many points these circles can have in common? What is the maximum number of common points?
Use the figure given below to fill in the blank:
________ is a radius of the circle.
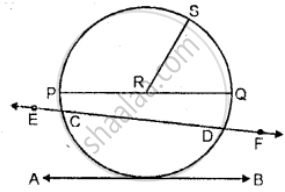
Use the figure given below to fill in the blank:
AB is a ______ of the circle.

A point A is 26 cm away from the centre of a circle and the length of the tangent drawn from A to the circle is 24 cm. Find the radius of the circle.