Advertisements
Advertisements
Question
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
Sum
Solution
Given: CD and EF are two parallel tangents at the points A and B of a circle with centre O.
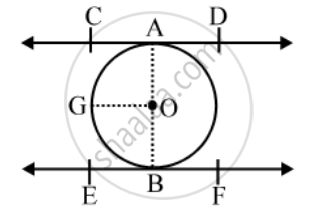
To prove: AOB is a diameter of the circle.
Construction: Join OA and OB.
Draw OG || CD
Proof: OG || CD and AO cuts them.
∴ ∠CAO + ∠GOA = 180°
⇒ ∠GOA = 180°
⇒ ∠GOA = 90°
Similarly, ∠GOB = 90°
∴ ∠GOA + ∠GOB = (90° + 90°) = 180°
⇒ AOB is a straight line
Hence, AOB is a diameter of the circle with centre O.
shaalaa.com
Is there an error in this question or solution?
