Advertisements
Advertisements
Question
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
Solution
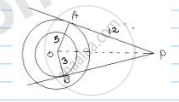
OA = 5 cm
OB = 3 cm
AP = 12 cm
BP = ?
We know that
At the point of contact, radius is perpendicular to tangent.
For circle 1, ΔOAP is right triangle
By Pythagoras theorem, ๐๐2 = ๐๐ด2 + ๐ด๐2
⇒ ๐๐2 = 52 + 122 = 25 + 144
= 169
⇒ OP = `sqrt(169)` = 13 ๐๐
For circle 2, ΔOBP is right triangle by Pythagoras theorem,
๐๐2 = ๐๐ต2 + ๐ต๐2
132 = 32 + ๐ต๐2
๐ต๐2 = 169 − 9 = 160
๐ต๐ = `sqrt(160) = 4sqrt(10)` ๐๐
APPEARS IN
RELATED QUESTIONS
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.
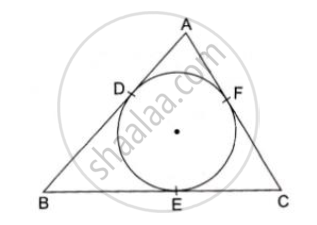
In the given figure, the incircle of โABC touches the sides BC, CA and AB at D, E, F respectively. Prove that AF + BD + CE = AE + CD + BF = `\frac { 1 }{ 2 } ("perimeter of โABC")`
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
Prove that two different circles cannot intersect each other at more than two points.
In the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F Respectively. If AB= 12cm, BC=8cm and AC = 10cm, find the length of AD, BE and CF.
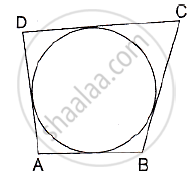
In the adjoining figure, a circle touches all the four sides of a quadrilateral ABCD whose sides are AB=6cm, BC=9cm and CD=8 cm. Find the length of side AD.
If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.
A chord is at a distance of 15 cm from the centre of the circle of radius 25 cm. The length of the chord is
If A, B, C, D are four points such that ∠BAC = 30° and ∠BDC = 60°, then D is the centre of the circle through A, B and C.
From the figure, identify the centre of the circle.
