Advertisements
Advertisements
рдкреНрд░рд╢реНрди
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
рдЙрддреНрддрд░
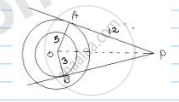
OA = 5 cm
OB = 3 cm
AP = 12 cm
BP = ?
We know that
At the point of contact, radius is perpendicular to tangent.
For circle 1, ΔOAP is right triangle
By Pythagoras theorem, ЁЭСВЁЭСГ2 = ЁЭСВЁЭР┤2 + ЁЭР┤ЁЭСГ2
⇒ ЁЭСВЁЭСГ2 = 52 + 122 = 25 + 144
= 169
⇒ OP = `sqrt(169)` = 13 ЁЭСРЁЭСЪ
For circle 2, ΔOBP is right triangle by Pythagoras theorem,
ЁЭСВЁЭСГ2 = ЁЭСВЁЭР╡2 + ЁЭР╡ЁЭСГ2
132 = 32 + ЁЭР╡ЁЭСГ2
ЁЭР╡ЁЭСГ2 = 169 − 9 = 160
ЁЭР╡ЁЭСГ = `sqrt(160) = 4sqrt(10)` ЁЭСРЁЭСЪ
APPEARS IN
рд╕рдВрдмрдВрдзрд┐рдд рдкреНрд░рд╢реНтАНрди
In Fig. 2, AB is the diameter of a circle with centre O and AT is a tangent. If ∠AOQ = 58°, find ∠ATQ.
The lengths of three consecutive sides of a quadrilateral circumscribing a circle are 4cm,5cm and 7cm respectively. Determine the length of fourth side.
Suppose You Are Given a Circle. Give a Construction to Find Its Centre.
O is the centre of a circle of radius 10 cm. P is any point in the circle such that OP = 6 cm. A is the point travelling along the circumference. x is the distance from A to P. what are the least and the greatest values of x in cm? what is the position of the points O, P and A at these values?
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
AB and CD are two equal chords of a drde intersecting at Pas shown in fig. P is joined to O , the centre of the cirde. Prove that OP bisects ∠ CPB.
In the given figure, O is the centre of a circle, chord PQ ≅ chord RS If ∠ POR = 70° and (arc RS) = 80°, find –
(1) m(arc PR)
(2) m(arc QS)
(3) m(arc QSR)
Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
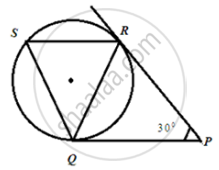
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
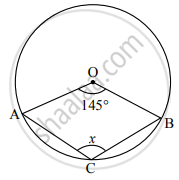
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.
