Advertisements
Advertisements
प्रश्न
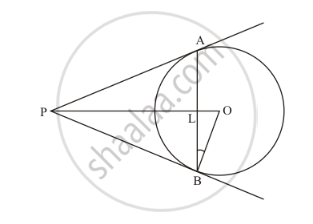
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
उत्तर
Consider ΔPOB and ΔPOA.

From the property of tangents we know that the length of two tangents drawn form an external point will be equal. Therefore we have,
PA = PB
OB = OA (They are the radii of the same circle)
PO is the common side
Therefore, from SSS postulate of congruency, we have,
ΔPOB and ΔPOA
Hence,
ΔOPA = ΔOPB …… (1)
Now consider ΔPLA and ΔPLB. We have,
∠OPA = ∠OPB (From (1)
PA is the common side.
From the property of tangents we know that the length of two tangents drawn form an external point will be equal. Therefore we have,
PA = PB
From SAS postulate of congruent triangles, we have,
ΔPLA ≅ ΔPLB
Therefore,
LA = LB
It is given that AB = 16. That is,
LA + LB = 16
LA + LA = 16
2LA = 16
LA = 8
LB = 8
Also, ALB is a straight line. Therefore
∠ALB = 180°
That is,
∠PLA+∠PLB=180°
Since ΔPLA=ΔPLB
∠PLA=∠PLB
Therefore,
2∠PLB=180°
∠PLB=90°
Now let us consider ΔOLB. We have,
`OL^2=OB^2-OL^2`
`OL^2=10^2-8^2`
`OL^2=100-64`
`OL^2=36`
OL=6
Consider ΔOPB Here,
∠OBP=90° (Since the radius of the circle will always be perpendicular to the tangent
at the point of contact)
Therefore,
`PB^2=OP^2-OB^2` …… (1)
Now consider ΔPLB
`PB^2=PL^2+BL^2` …… (2)
Since the Left Hand Side of equation (1) is same as the Left Hand Side of equation
(2), we can equate the Right Hand Side of the two equations. Hence we have,
`OP^2-OB^2= PL^2+LB^2` …… (3)
From the figure we can see that,
OP = OL + LP
Therefore, let us replace OP with OL + LP in equation (3). We have,
`(OL+PL)^2-OB^2-PL^2+LB^2`
We have found that OL = 6 and LB = 8. Also it is given that OB = 10. Substituting all
these values in the above equation, we get,
`(6+PL)^2-10^2=PL^2+8^2`
`36+PL^2+2xx6xxPL-100=PL^2+64`
12PL=128
`PL=32/3`
Now, let us substitute the value of PL in equation (2). We get,
`PB^2=(32/3)^2+8^2`
`PB^2=(1024)/9+64`
`PB^2=(1600)/9`
`PB=sqrt((1600)/9)`
`PB=40/3`
We know that tangents drawn from an external point will always be equal. Therefore,
PB = PA
Hence, we have,
`PB=40/3`
APPEARS IN
संबंधित प्रश्न
From a point P, 10 cm away from the centre of a circle, a tangent PT of length 8 cm is drawn. Find the radius of the circle.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

The point of concurrence of all angle bisectors of a triangle is called the ______.
Use the figure given below to fill in the blank:
________ is a radius of the circle.
Can the length of a chord of a circle be greater than its diameter ? Explain.
State, if the following statement is true or false:
Every diameter bisects a circle and each part of the circle so obtained is a semi-circle.
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
A point P is 10 cm from the center of a circle. The length of the tangent drawn from P to the circle is 8 cm. The radius of the circle is equal to ______
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]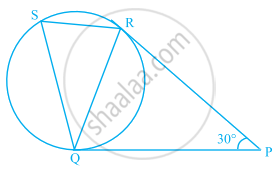
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

