Advertisements
Advertisements
प्रश्न
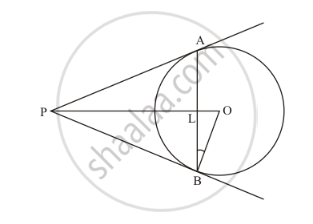
In the given figure, AB is a chord of length 16 cm of a circle of radius 10 cm. The tangents at A and B intersect at a point P. Find the length of PA.
उत्तर
Consider ΔPOB and ΔPOA.

From the property of tangents we know that the length of two tangents drawn form an external point will be equal. Therefore we have,
PA = PB
OB = OA (They are the radii of the same circle)
PO is the common side
Therefore, from SSS postulate of congruency, we have,
ΔPOB and ΔPOA
Hence,
ΔOPA = ΔOPB …… (1)
Now consider ΔPLA and ΔPLB. We have,
∠OPA = ∠OPB (From (1)
PA is the common side.
From the property of tangents we know that the length of two tangents drawn form an external point will be equal. Therefore we have,
PA = PB
From SAS postulate of congruent triangles, we have,
ΔPLA ≅ ΔPLB
Therefore,
LA = LB
It is given that AB = 16. That is,
LA + LB = 16
LA + LA = 16
2LA = 16
LA = 8
LB = 8
Also, ALB is a straight line. Therefore
∠ALB = 180°
That is,
∠PLA+∠PLB=180°
Since ΔPLA=ΔPLB
∠PLA=∠PLB
Therefore,
2∠PLB=180°
∠PLB=90°
Now let us consider ΔOLB. We have,
`OL^2=OB^2-OL^2`
`OL^2=10^2-8^2`
`OL^2=100-64`
`OL^2=36`
OL=6
Consider ΔOPB Here,
∠OBP=90° (Since the radius of the circle will always be perpendicular to the tangent
at the point of contact)
Therefore,
`PB^2=OP^2-OB^2` …… (1)
Now consider ΔPLB
`PB^2=PL^2+BL^2` …… (2)
Since the Left Hand Side of equation (1) is same as the Left Hand Side of equation
(2), we can equate the Right Hand Side of the two equations. Hence we have,
`OP^2-OB^2= PL^2+LB^2` …… (3)
From the figure we can see that,
OP = OL + LP
Therefore, let us replace OP with OL + LP in equation (3). We have,
`(OL+PL)^2-OB^2-PL^2+LB^2`
We have found that OL = 6 and LB = 8. Also it is given that OB = 10. Substituting all
these values in the above equation, we get,
`(6+PL)^2-10^2=PL^2+8^2`
`36+PL^2+2xx6xxPL-100=PL^2+64`
12PL=128
`PL=32/3`
Now, let us substitute the value of PL in equation (2). We get,
`PB^2=(32/3)^2+8^2`
`PB^2=(1024)/9+64`
`PB^2=(1600)/9`
`PB=sqrt((1600)/9)`
`PB=40/3`
We know that tangents drawn from an external point will always be equal. Therefore,
PB = PA
Hence, we have,
`PB=40/3`
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.
In the given circle with diameter AB, find the value of x.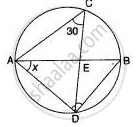
Use the figure given below to fill in the blank:
R is the _______ of the circle.

Construct a triangle PQR with QR = 5.5 cm, ∠Q = 60° and angle R = 45°. Construct the circumcircle cif the triangle PQR.
Construct a triangle XYZ in which XY = YZ= 4.5 cm and ZX = 5.4 cm. Draw the circumcircle of the triangle and measure its circumradius.
If the angle between two radii of a circle is 130°, then the angle between the tangents at the ends of the radii is ______
In the following figure, ∠OAB = 30º and ∠OCB = 57º. Find ∠BOC and ∠AOC.

In the given figure, O is the centre of the circle. Shade the smaller segment of the circle formed by CP.