Advertisements
Advertisements
प्रश्न
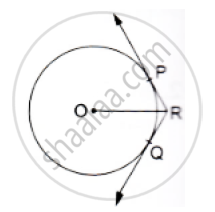
In the given figure, two tangents RQ, and RP and RP are drawn from an external point R to the circle with centre O. If ∠PRQ =120° , then prove that OR = PR + RQ.
उत्तर

Construction Join PO and OQ
In ΔPOR and ΔQOR
OP = OQ(Radii)
RP = RQ(Tangents from the external point are congruent)
OR = OR (Common)
By SSS congruency, ΔPOR ≅ ΔQOR
∠PRO = ∠QRO(C.P.C.T)
Now,∠PRO+ ∠QRO= ∠PRQ
⇒ 2 ∠PRO = 120°
⇒ ∠PRO = 60°
Now. In ΔPOR
cos 60° `=(PR)/(OR)`
⇒ `1/2 =(PR)/(OR)`
⇒ OR = 2PR
⇒ OR = PR + PR
⇒ OR = PR +RQ
APPEARS IN
संबंधित प्रश्न
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
Two tangent segments PA and PB are drawn to a circle with center O such that ∠APB =120°. Prove that OP = 2AP
If O is the centre of a circle of radius r and AB is a chord of the circle at a distance r/2 from O, then ∠BAO =
If AB, BC and CD are equal chords of a circle with O as centre and AD diameter, than ∠AOB =
In the given figure, a ∆ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC are of lengths 8 cm and 6 cm respectively. Find the lengths of sides AB and AC, when area of ∆ABC is 84 cm2.

Draw a circle of radius of 4.2 cm. Mark its center as O. Takes a point A on the circumference of the circle. Join AO and extend it till it meets point B on the circumference of the circle,
(i) Measure the length of AB.
(ii) Assign a special name to AB.
Find the diameter of the circle
Radius = 8 cm
In the figure, O is the centre of a circle, AB is a chord, and AT is the tangent at A. If ∠AOB = 100°, then ∠BAT is equal to ______

The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
If AB is a chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT = ∠ACB