Advertisements
Advertisements
प्रश्न
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
विकल्प
True
False
उत्तर
This statement is True.
Explanation:
Let EAF be tangent to the circumcircle of ∆ABC.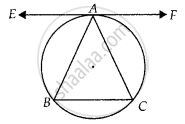
To prove: EAF ॥ BC
We have, ∠EAB = ∠ACB ...(i) [Angle between tangent and chord is equal to angle made by chord in the alternate segment]
Here, AB = AC
⇒ ∠ABC = ∠ACB ...(ii)
From equation (i) and (ii), we get
∠EAB = ∠ABC
∵ Alternate angles are equal.
⇒ EAF ॥ BC
APPEARS IN
संबंधित प्रश्न
Prove that the line segment joining the point of contact of two parallel tangents to a circle is a diameter of the circle.
ABC is a right triangle, right angled at B. A circle is inscribed in it. The lengths of the two sides containing the right angle are 6 cm and 8 cm. Find the radius of the incircle.
In Fig., if AB = AC, prove that BE = EC
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

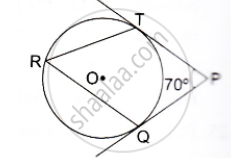
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
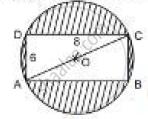
Find the area of the shaded region in the figure If ABCD is a rectangle with sides 8 cm and 6 cm and O is the centre of the circle. (Take π= 3.14)
Use the figure given below to fill in the blank:
______ is a chord of the circle.

Use the figure given below to fill in the blank:
If the length of RS is 5 cm, the length of PQ = _______

A quadrilateral ABCD is inscribed in a circle such that AB is a diameter and ∠ADC = 130º. Find ∠BAC.
A 7 m broad pathway goes around a circular park with a circumference of 352 m. Find the area of road.
