Advertisements
Advertisements
Question
The tangent to the circumcircle of an isosceles triangle ABC at A, in which AB = AC, is parallel to BC.
Options
True
False
Solution
This statement is True.
Explanation:
Let EAF be tangent to the circumcircle of ∆ABC.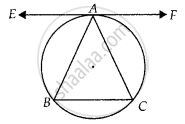
To prove: EAF ॥ BC
We have, ∠EAB = ∠ACB ...(i) [Angle between tangent and chord is equal to angle made by chord in the alternate segment]
Here, AB = AC
⇒ ∠ABC = ∠ACB ...(ii)
From equation (i) and (ii), we get
∠EAB = ∠ABC
∵ Alternate angles are equal.
⇒ EAF ॥ BC
APPEARS IN
RELATED QUESTIONS
A chord of a circle of radius 10 em subtends a right angle at its centre. The length of the chord (in em) is
`(A) 5sqrt 2`
`(B) 10 sqrt2`
`(C)5/sqrt2`
`(D) 10sqrt 3`
In Fig. 8, O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects circle at E. If AB is a tangent to the circle at E, find the length of AB, where TP and TQ are two tangents to the circle.

ture or false v
The degree measure of a semi-circle is 180°.
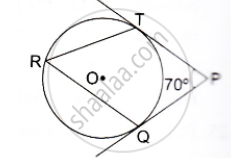
In the given figure, O is the centre of a circle. PT and PQ are tangents to the circle from an external point P. If ∠TPQ = 70° , find the ∠TRQ.
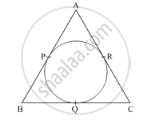
In Fig. 1, the sides AB, BC and CA of a triangle ABC, touch a circle at P, Q and R respectively. If PA = 4 cm, BP = 3 cm and AC = 11 cm, then the length of BC (in cm) is ?
Find the diameter of the circle
Radius = 8 cm
Circles with centres A, B and C touch each other externally. If AB = 3 cm, BC = 3 cm, CA = 4 cm, then find the radii of each circle.
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
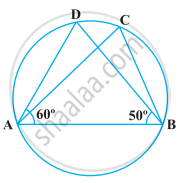
In the following figure, if ∠DAB = 60º, ∠ABD = 50º, then ∠ACB is equal to ______.
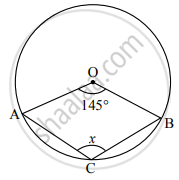
In the given figure, O is the centre of the circle. If ∠ AOB = 145°, then find the value of x.