Advertisements
Advertisements
Question
If a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular bisector of PQ.
Options
True
False
Solution
This statement is False.
Explanation:
Given that PQ is any line segment and S1, S2, S3, S4,... circles are touch a line segment PQ at a point A.
Let the centres of the circles S1, S2, S3, S4,... be C1, C2, C3, C4,... respectively.
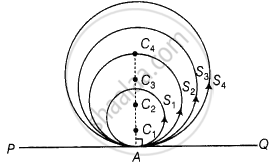
To prove centres of these circles lie on the perpendicular bisector PQ.
Now, joining each centre of the circles to the point A on the line segment PQ by a line segment i.e., C1A, C2A, C3A, C4A... so on.
We know that, if we draw a line from the centre of a circle to its tangent line, then the line is always perpendicular to the tangent line.
But it not bisect the line segment PQ.
So,
C1A ⊥ PQ ...[For S1]
C2A ⊥ PQ ...[For S2]
C3A ⊥ PQ ...[For S3]
C4A ⊥ PQ ...[For S4]
Since, each circle is passing through a point A.
Therefore, all the line segments C1A, C2A, C3A, C4A.... so on are coincident.
So, centre of each circle lies on the perpendicular line of PQ but they do not lie on the perpendicular bisector of PQ.
Hence, a number of circles touch a given line segment PQ at a point A, then their centres lie on the perpendicular of PQ but not on the perpendicular bisector of PQ.
APPEARS IN
RELATED QUESTIONS
In the given figure, a circle with center O, is inscribed in a quadrilateral ABCD such that it touches the side BC, AB, AD and CD at points P, Q, R and S respectively. If AB = 29cm, AD = 23cm, ∠B = 90° and DS=5cm then find the radius of the circle.

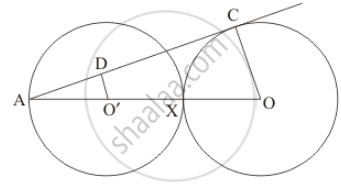
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
In Fig. 8.79, PQ is a tangent from an external point P to a circle with centre O and OP cuts the circle at T and QOR is a diameter. If ∠POR = 130° and S is a point on the circle, find ∠1 + ∠2.


In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
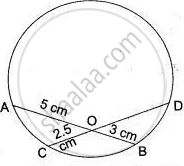
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
Use the figure given below to fill in the blank:
EF is a ______ of the circle.

State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
Find the diameter of the circle
Radius = 8 cm
In the figure, a circle with center P touches the semicircle at points Q and C having center O. If diameter AB = 10, AC = 6, then find the radius x of the smaller circle.
In the following figure, if AOB is a diameter of the circle and AC = BC, then ∠CAB is equal to ______.

