Advertisements
Advertisements
Question
In Fig., chords AB and CD of the circle intersect at O. AO = 5 cm, BO = 3 cm and CO = 2.5 cm. Determine the length of DO.
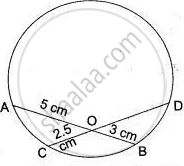
Solution
Given:
AO = 5 cm
BO = 3 cm
CO = 2.5 cm
We need to find the length of DO.
From the Intersecting Chords Theorem (or Power of a Point Theorem), we know:
Product of segments of one chord = Product of segments of the other chord
Clearly, chords AB and CD intersect at O.
∴ AO × BO = CO × DO
⇒ 5 × 3 = 2.5 × DO
⇒ DO = `(( 5 xx 3)/2.5)`
= 6 cm.
The length of DO is 6 cm.
APPEARS IN
RELATED QUESTIONS
A point P is 13 cm from the centre of the circle. The length of the tangent drawn from P to the circle is 12cm. Find the radius of the circle.
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
In the given figure, a circle touches all the four sides of a quadrilateral ABCD whose three sides are AB = 6cm, BC=7cm and CD=4 cm. Find AD.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.

In the given figure, PA and PB are two tangents to the circle with centre O. If ∠APB = 60° then find the measure of ∠OAB.

In the given figure, chord EF || chord GH. Prove that, chord EG ≅ chord FH. Fill in the blanks and write the proof.

Find the diameter of the circle
Radius = 6 cm
Prove that angle bisector of any angle of a triangle and perpendicular bisector of the opposite side if intersect, they will intersect on the circumcircle of the triangle.
Is every diameter of a circle also a chord?
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
