Advertisements
Advertisements
Question
Find the length of the arc of a circle which subtends an angle of 60° at the centre of the circle of radius 42 cm.
Solution
Substituting the given values into the formula:
Arc length = `(60°)/(360°) xx 2 xx π xx 42 cm`
Arc length = `1/6 xx 2 xx π xx 42 cm`
Arc length= `1/3 xx 42 cm`
Arc length = `42/3 xx π cm`
Arc length = 14 × π cm
Since π ≈ 3.14159, we have:
Arc length = 14 × 3.14159 cm
Therefore, the length of the arc is approximately 43.98 cm.
APPEARS IN
RELATED QUESTIONS
In fig. XP and XQ are tangents from X to the circle with centre O. R is a point on the circle. Prove that, XA + AR = XB + BR.
Two concentric circles are of radii 6.5 cm and 2.5 cm. Find the length of the chord of the larger circle which touches the smaller circle.
The circumference of a circle is 22 cm. The area of its quadrant (in cm2) is
In the given figure, PO \[\perp\] QO. The tangents to the circle at P and Q intersect at a point T. Prove that PQ and OTare right bisector of each other.

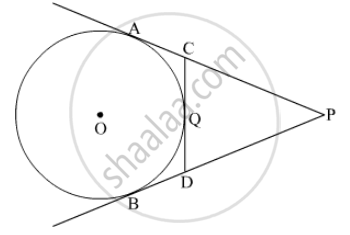
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Find the length of the chord of a circle in the following when:
Radius is 1. 7cm and the distance from the centre is 1.5 cm
Draw a circle of radius 6 cm. In the circle, draw a chord AB = 6 cm.
(i) If O is the center of the circle, join OA and OB.
(ii) Assign a special name to ∆AOB
(iii) Write the measure of angle AOB.
Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
If a chord AB subtends an angle of 60° at the centre of a circle, then the angle between the tangents at A and B is ______
In the given figure, O is the centre of the circle. Name all chords of the circle.