Advertisements
Advertisements
Question
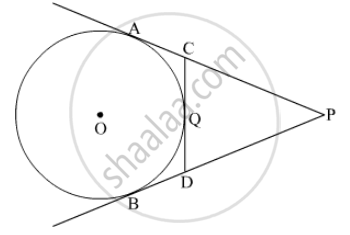
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Solution
Given: PA and PB are the tangents to the circle.
PA = 12 cm
QC = QD = 3 cm
To find: PC + PD
PA = PB = 12 cm (The lengths of tangents drawn from an external point to a circle are equal)
Similarly, QC = AC = 3 cm
and QD = BD = 3 cm.
Now, PC = PA − AC = 12 − 3 = 9 cm
Similarly, PD = PB − BD = 12 − 3 = 9 cm
Hence, PC + PD = 9 + 9 = 18 cm.
APPEARS IN
RELATED QUESTIONS
Write True or False. Give reasons for your answers.
A chord of a circle, which is twice as long as its radius, is a diameter of the circle.
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
A point P is 26 cm away from O of circle and the length PT of the tangent drawn from P to the circle is 10 cm. Find the radius of the circle.
If the difference between the circumference and the radius of a circle is 37 cm, then using`22/7`, the circumference (in cm) of the circle is:
Find the area of a circle of radius 7 cm.

In the above figure, seg AB is a diameter of a circle with centre P. C is any point on the circle. seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of the following steps:
a. Draw ray CE. It intersects the circle at D.
b. Show that CE = ED.
c. Write the result using the theorem of the intersection of chords inside a circle. d. Using CE = ED, complete the proof.
Draw a line AB = 8.4 cm. Now draw a circle with AB as diameter. Mark a point C on the circumference of the circle. Measure angle ACB.
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
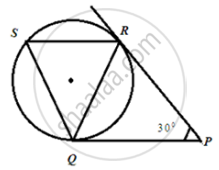
In the following figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ, then ∠RQS.
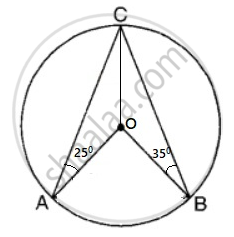
In the adjoining figure ‘O’ is the center of the circle, ∠CAO = 25° and ∠CBO = 35°. What is the value of ∠AOB?