Advertisements
Advertisements
Question
If PT is a tangent at T to a circle whose center is O and OP = 17 cm, OT = 8 cm. Find the length of tangent segment PT.
Solution
OT = radius = 8cm
OP = 17cm
PT = length of tangent = ?
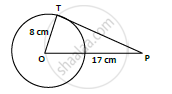
T is point of contact. We know that at point of contact tangent and radius are perpendicular.
∴ OTP is right angled triangle ∠OTP = 90°, from Pythagoras theorem 𝑂𝑇2 + 𝑃𝑇2 = 𝑂𝑃2
82 + 𝑃𝑇2 = 172
`PT sqrt(17^2 − 8^2) = sqrt(289 − 64)`
=`sqrt(225)` = 15𝑐𝑚
∴ PT = length of tangent = 15 cm.
APPEARS IN
RELATED QUESTIONS
In fig.. O is the center of the circle and BCD is tangent to it at C. Prove that ∠BAC +
∠ACD = 90°
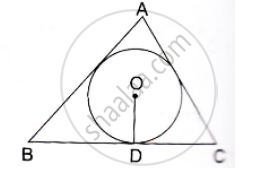
In the given figure, a triangle ABC is drawn to circumscribe a circle of radius 2 cm such that the segments BD and DC into which BC is divided by the point of contact D, are of lengths 4cm and 3cm respectively. If the area of 2 ABC 21cm then find the lengths of sides AB and AC.
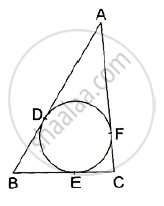
In the given figure, a cradle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14cm, BC = 8cm and CA=12 cm. Find the length AD, BE and CF.
Two circles touch internally. The sum of their areas is 116 π cm2 and the distance between their centres is 6 cm. Find the radii of the circles ?
State, if the following statement is true or false:
If the end points A and B of the line segment lie on the circumference of a circle, AB is a diameter.
Find the diameter of the circle
Radius = 6 cm
In the figure, segment PQ is the diameter of the circle with center O. The tangent to the tangent circle drawn from point C on it, intersects the tangents drawn from points P and Q at points A and B respectively, prove that ∠AOB = 90°
In the following figure, ∠AOB = 90º and ∠ABC = 30º, then ∠CAO is equal to ______.

Two chords AB and AC of a circle subtends angles equal to 90º and 150º, respectively at the centre. Find ∠BAC, if AB and AC lie on the opposite sides of the centre.
From the figure, identify three radii.