Advertisements
Advertisements
Question
Find the length of a tangent drawn to a circle with radius 5cm, from a point 13 cm from the center of the circle.
Solution
Consider a circle with center O.
OP = radius = 5 cm.
A tangent is drawn at point P, such that line through O intersects it at Q, OB = 13cm.
Length of tangent PQ = ?
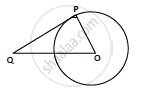
A + P, we know that tangent and radius are perpendicular.
Δ๐๐๐ is right angled triangle, ∠OPQ = 90°
๐ต๐ฆ ๐๐ฆ๐กโ๐๐๐๐๐๐ ๐กโ๐๐๐๐๐, ๐๐2 = ๐๐2 + ๐๐2
⇒ 132 = 52 + ๐๐2
⇒ ๐๐2 = 169 − 25 = 144
⇒ PQ =` sqrt(144)` = 12๐๐
Length of tangent = 12 cm
APPEARS IN
RELATED QUESTIONS
true or false
Sector is the region between the chord and its corresponding arc.
In the given figure, O is the centre of the circle and TP is the tangent to the circle from an external point T. If ∠PBT = 30° , prove that BA : AT = 2 : 1.
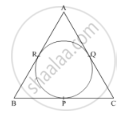
In Fig. 4, an isosceles triangle ABC, with AB = AC, circumscribes a circle. Prove that the point of contact P bisects the base BC.
A chord of length 14 cm is at a distance of 6 cm from the centre of a circle. The length of another chord at a distance of 2 cm from the centre of the circle is
Find the length of the chord of a circle in the following when:
Radius is 13 cm and the distance from the centre is 12 cm
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
(a) OP = 10.6 cm
(b) OP = 6.8 cm
(c) OP = 8 cm
In the figure, O is the center of the circle. Line AQ is a tangent. If OP = 3, m(arc PM) = 120°, then find the length of AP.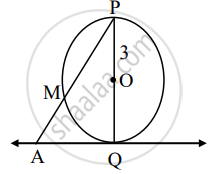
In the following figure, ∠ADC = 130° and chord BC = chord BE. Find ∠CBE.
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
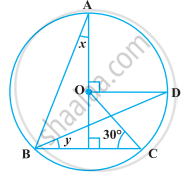
In the following figure, O is the centre of the circle, ∠BCO = 30°. Find x and y.
