Advertisements
Advertisements
Question
The center of a circle is at point O and its radius is 8 cm. State the position of a point P (point P may lie inside the circle, on the circumference of the circle, or outside the circle), when:
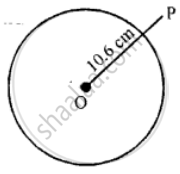
(a) OP = 10.6 cm
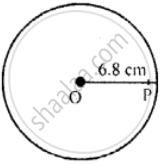
(b) OP = 6.8 cm
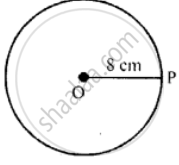
(c) OP = 8 cm
Solution
(a) Draw circle each of radius 8 cm. With centre O In the following figure (i) draw OP = 10.6 cm
(i)
(ii)
(iii)
We see that point P lies outside the circle as OP > radius of the circle
(b) In the above figure (ii) OP = 6.8 cm. We see that P lies inside the circle as OP < radius of the circle.
(c) In the above figure, OP = 8 cm. We see that P lies on the circle as OP = radius of the circle.
APPEARS IN
RELATED QUESTIONS
If PA and PB are tangents from an outside point P. such that PA = 10 cm and ∠APB = 60°. Find the length of chord AB.
In fig. there are two concentric circles with Centre O of radii 5cm and 3cm. From an
external point P, tangents PA and PB are drawn to these circles if AP = 12cm, find the
tangent length of BP.
In the given figure, O is the centre of the circle. If ∠AOB = 140° and ∠OAC = 50°; find:
- ∠ACB,
- ∠OBC,
- ∠OAB,
- ∠CBA.

In the given figure, the chord AB of the larger of the two concentric circles, with center O, touches the smaller circle at C. Prove that AC = CB.
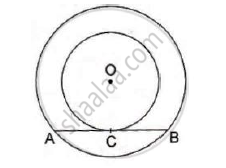
In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

If ABCD is a cyclic quadrilateral in which AD || BC (In the given figure). Prove that ∠B = ∠C.


In the above figure, `square`XLMT is a rectangle. LM = 21 cm, XL = 10.5 cm. Diameter of the smaller semicircle is half the diameter of the larger semicircle. Find the area of non-shaded region.
Suppose you are given a circle. Describe a method by which you can find the center of this circle.
Use the figure given below to fill in the blank:
______ is a chord of the circle.

Three circles touch each other externally. The distance between their centres is 5 cm, 6 cm, and 7 cm. Find the radii of the circles.
