Advertisements
Advertisements
Question
If ABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C, prove that PA is angle bisector of ∠BPC.
Solution
Given: ΔABC is an equilateral triangle inscribed in a circle and P be any point on the minor arc BC which does not coincide with B or C.
To prove: PA is an angle bisector of ∠BPC.
Construction: Join PB and PC.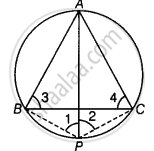
Proof: Since, ΔABC is an equilateral triangle.
∠3 = ∠4 = 60°
Now, ∠1 = ∠4 = 60° ...(i) [Angles in the same segment AB]
∠2 = ∠3 = 60° ...(ii) [Angles in the same segment AC]
∴ ∠1 = ∠2 = 60°
Hence, PA is the bisector of ∠BPC.
Hence proved.
APPEARS IN
RELATED QUESTIONS
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
true or false
Sector is the region between the chord and its corresponding arc.
Prove that two different circles cannot intersect each other at more than two points.
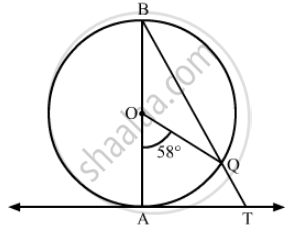
In the given figure, AB is a diameter of a circle with centre O and AT is a tangent. If \[\angle\] AOQ = 58º, find \[\angle\] ATQ.
Draw circle with the radii given below.
2 cm
A chord is 12 cm away from the centre of the circle of radius 15 cm. Find the length of the chord
In the figure, O is the centre of the circle, and ∠AOB = 90°, ∠ABC = 30°. Then find ∠CAB.

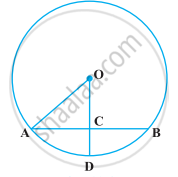
In the following figure, if OA = 5 cm, AB = 8 cm and OD is perpendicular to AB, then CD is equal to ______.
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
In the given figure, O is the centre of the circle. Name all chords of the circle.