Advertisements
Advertisements
Question
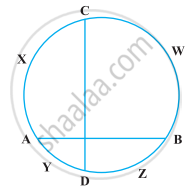
If two chords AB and CD of a circle AYDZBWCX intersect at right angles (see figure), prove that arc CXA + arc DZB = arc AYD + arc BWC = semi-circle.
Solution
Given: In a circle AYDZBWCX, two chords AB and CD intersect at right angles.
To prove: arc CXA + arc DZB = arc AYD + arc BWC = Semi-circle.
Construction: Draw a diameter EF parallel to CD having centre M.
Proof: Since, CD || EF
arc EC = arc PD ...(i)
arc ECXA = arc EWB [Symmetrical about diameter of a circle]
arc AF = arc BF ...(ii)
We know that, ar ECXAYDF = Semi-circle
arc EA + arc AF = Semi-circle
⇒ arc EC + arc CXA = arc FB = Semi-circle ...[From equation (ii)]
⇒ arc DF + arc CXA + arc FB = Semi-circle ...[From equation (i)]
⇒ arc DF + arc FB + arc CXA = Semi-circle
⇒ arc DZB + arc C × A = Semi-circle
We know that, circle divides itself in two semi-circles, therefore the remaining portion of the circle is also equal to the semi-circle.
∴ arc AYD + arc BWC = Semi-circle
Hence proved.
APPEARS IN
RELATED QUESTIONS
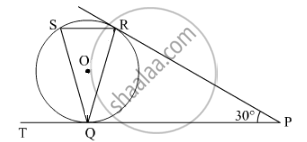
In the given figure, tangents PQ and PR are drawn from an external point P to a circle with centre O, such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find ∠RQS.
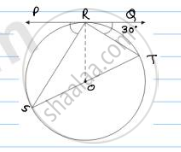
In Fig below, PQ is tangent at point R of the circle with center O. If ∠TRQ = 30°. Find
∠PRS.
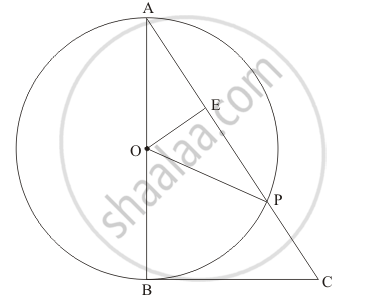
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO~Δ ABC.

In the given figure, O is the centre of the circle. PA and PB are tangents. Show that AOBP is cyclic quadrilateral.

In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
Use the figure given below to fill in the blank:
Diameter of a circle is ______.

Draw a circle of radius 3.6 cm. In the circle, draw a chord AB = 5 cm. Now shade the minor segment of the circle.
Find the missing values in the following table for the circles with radius (r), diameter (d) and Circumference (C).
| radius (r) | diameter (d) | Circumference (C) |
| 1760 cm |
If the angle between two tangents drawn from a point P to a circle of radius ‘a’ and centre ‘O’ is 90°, then OP = ______
AB and AC are two equal chords of a circle. Prove that the bisector of the angle BAC passes through the centre of the circle.
