Advertisements
Advertisements
Question
In the given figure, BC is a tangent to the circle with centre O. OE bisects AP. Prove that ΔAEO ∼ Δ ABC.
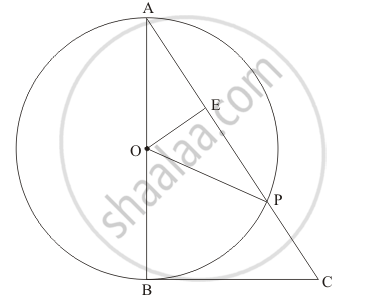
Solution
The figure given in the question is below
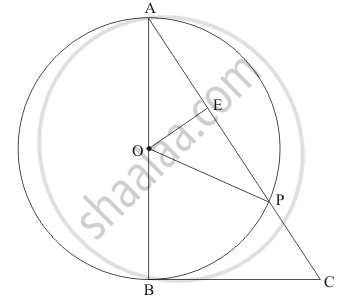
Let us first take up Δ AOP.
We have,
OA = OP (Since they are the radii of the same circle)
Therefore, Δ AOP. is an isosceles triangle. From the property of isosceles triangle, we know that, when a median drawn to the unequal side of the triangle will be perpendicular to the unequal side. Therefore,
`∠ OEA=90^o`
Now let us take up Δ AOE and Δ ABC..
We know that the radius of the circle will always be perpendicular to the tangent at the point of contact. In this problem, OB is the radius and BC is the tangent and B is the point of contact. Therefore,
`∠ ABC=90^o`
Also, from the property of isosceles triangle we have found that
`∠ OEA = 90^o`
Therefore,
`∠ ABC`= `∠ OEA`
`∠ A` is the common angle to both the triangles.
Therefore, from AA postulate of similar triangles,
`ΔAOE` ~ `ΔABC`
Thus we have proved.
APPEARS IN
RELATED QUESTIONS
Fill in the blanks:
A point, whose distance from the centre of a circle is greater than its radius lies in __________ of the circle. (exterior/ interior)
If AB, AC, PQ are tangents in Fig. and AB = 5cm find the perimeter of ΔAPQ.
In the fig two tangents AB and AC are drawn to a circle O such that ∠BAC = 120°. Prove that OA = 2AB.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of:
- ∠AOB,
- ∠ACB,
- ∠ABC.
A circle is inscribed in a ΔABC touching AB, BC and AC at P, Q and R respectively. If AB = 10 cm, AR=7cm and CR=5cm, find the length of BC.

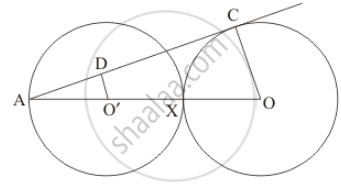
Equal circles with centres O and O' touch each other at X. OO' produced to meet a circle with centre O', at A. AC is a tangent to the circle whose centre is O. O'D is perpendicular to AC. Find the value of\[\frac{DO'}{CO}\]
Find the diameter of the circle
Radius = 8 cm
A line through the point of contact and passing through centre of the circle is known as ______
In figure, tangents PQ and PR are drawn to a circle such that ∠RPQ = 30°. A chord RS is drawn parallel to the tangent PQ. Find the ∠RQS.
[Hint: Draw a line through Q and perpendicular to QP.]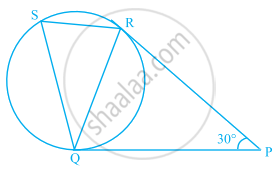
If AOB is a diameter of a circle and C is a point on the circle, then AC2 + BC2 = AB2.
